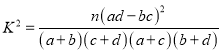题目内容
【题目】已知 ![]() =(m﹣2)
=(m﹣2) ![]() +2
+2 ![]() ,
, ![]() =
= ![]() +(m+1)
+(m+1) ![]() ,其中
,其中 ![]() 、
、 ![]() 分别为x、y轴正方向单位向量.
分别为x、y轴正方向单位向量.
(1)若m=2,求 ![]() 与
与 ![]() 的夹角;
的夹角;
(2)若( ![]() +
+ ![]() )⊥(
)⊥( ![]() ﹣
﹣ ![]() ),求实数m的值.
),求实数m的值.
【答案】
(1)解:因为 ![]() 、
、 ![]() 分别为x、y轴正方向单位向量,所以
分别为x、y轴正方向单位向量,所以 ![]() =(m﹣2,2),
=(m﹣2,2), ![]() =(1,m+1),
=(1,m+1),
所以(1)m=2时, ![]() =(0,2,),
=(0,2,), ![]() =(1,3),
=(1,3), ![]() 与
与 ![]() 的夹角的余弦值
的夹角的余弦值 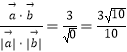 ,所以
,所以 ![]() 与
与 ![]() 的夹角为arccos
的夹角为arccos ![]()
(2)解: ![]() +
+ ![]() =(m﹣1,m+2),
=(m﹣1,m+2), ![]() ﹣
﹣ ![]() =(m﹣3,1﹣m),又(
=(m﹣3,1﹣m),又( ![]() +
+ ![]() )⊥(
)⊥( ![]() ﹣
﹣ ![]() ),所以(m﹣1)(m﹣3)+(m+2)(1﹣m)=0,即﹣5m+5=0,解得m=1
),所以(m﹣1)(m﹣3)+(m+2)(1﹣m)=0,即﹣5m+5=0,解得m=1
【解析】由已知,将 ![]() 与
与 ![]() 坐标化,利用平面向量的坐标运算解答即可.(1)将m代入两个向量的坐标,进行数量积的坐标运算即可;(2)分别求出
坐标化,利用平面向量的坐标运算解答即可.(1)将m代入两个向量的坐标,进行数量积的坐标运算即可;(2)分别求出 ![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]() 的坐标,利用向量垂直数量积为0,求出m.
的坐标,利用向量垂直数量积为0,求出m.
【考点精析】本题主要考查了平面向量的坐标运算的相关知识点,需要掌握坐标运算:设![]() ,
,![]() 则
则![]() ;
;![]() ;设
;设![]() ,则
,则![]() 才能正确解答此题.
才能正确解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了调查某高中学生每天的睡眠时间,现随机对20名男生和20名女生进行问卷调查,结果如下:
女生:
睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9] |
人数 | 2 | 4 | 8 | 4 | 2 |
男生:
睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9] |
人数 | 1 | 5 | 6 | 5 | 3 |
(1)现把睡眠时间不足5小时的定义为“严重睡眠不足”,从睡眠时间不足6小时的女生中随机抽取2人,求此2人中恰有一人为“严重睡眠不足”的概率;
(2)完成下面2×2列联表,并回答是否有90%的把握认为“睡眠时间与性别有关”?
睡眠时间少于7小时 | 睡眠时间不少于7小时 | 合计 | |
男生 | |||
女生 | |||
合计 |
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
( ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)