��Ŀ����
����Ŀ��2016����˻���8��5���ڰ�����Լ����¬���У�Ϊ�˽�ij��λԱ�����˻�Ĺ�ע������Ա���λ����Ա�������˵��飬�õ�ƽ��ÿ�쿴���˻�ֱ��ʱ��ľ�Ҷͼ���£���λ�����ӣ�����ƽ��ÿ�쿴���˻�ֱ��������70���ӵ�Ա��������Ϊ����ע���ˡ���������Ϊ������ע���ˡ�.
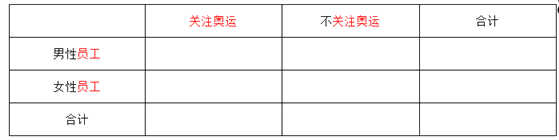
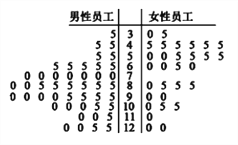
��1�����������������ݴ������ж��Ƿ���99.5%���ϵİ�����Ϊ�Ƿ�ע���˻ᡱ���Ա��йأ�
��2�����Ӳ��������ƽ��ÿ��ۿ����˻�ʱ�䲻����110���ӵ�Ա���г�ȡ4�ˣ���![]() ��ʾ��ȡ��ŮԱ��������
��ʾ��ȡ��ŮԱ��������![]() �ķֲ��к�����ֵ.
�ķֲ��к�����ֵ.
�ο���ʽ�� 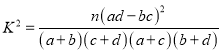 ������
������![]()
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡���1������������2��������.
�������������������1��������֪���������2��2������������K2�������ж��Ƿ���99.5%���ϵİ�����Ϊ�Ƿ�ע���ˡ����Ա��йأ�
��2���жϦεĿ���ȡֵ�У�0��1��2��3��������ʣ��õ��εķֲ��У�Ȼ������������ɣ�
���������
��1��![]() ���������£�
���������£�
��ע���� | ����ע���� | �ϼ� | |
����Ա�� | 35 | 10 | 45 |
Ů��Ա�� | 12 | 18 | 30 |
�ϼ� | 47 | 28 | 75 |
��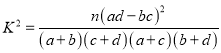
![]()
���ԣ���99.5%���ϵİ�����Ϊ�Ƿ�ע���˻ᡱ���Ա��й�.
��2����������֪�� ![]() �Ŀ���ȡֵ�У�0��1��2��3����
�Ŀ���ȡֵ�У�0��1��2��3����
![]() ��
�� ![]() ��
�� ![]() ��
�� ![]()
��![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
| 0 | 1 | 2 | 3 |
P |
|
|
|
|
Ů��Ա��������ֵΪ�� ![]() .
.