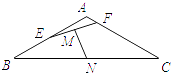题目内容
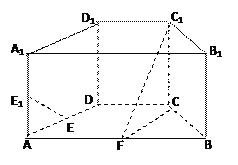
【题目】如图,在直四棱柱ABCD-A![]() B
B![]() C
C![]() D
D![]() 中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA
中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA![]() =2, E、E
=2, E、E![]() 、F分别是棱AD、AA
、F分别是棱AD、AA![]() 、AB的中点。
、AB的中点。
证明:(1)直线EE![]() //平面FCC
//平面FCC![]() ;
;
(2)求二面角B-FC![]() -C的余弦值。
-C的余弦值。
【答案】(1)见解析 (2) ![]()
【解析】试题分析:(1)以DM为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,求得设平面CC1F的法向量为![]() ,
, 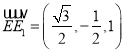 ,由
,由![]() 得直线EE
得直线EE![]() //平面FCC
//平面FCC![]() ;
;
(2)通过建立空间直角坐标系,先求出两个平面的法向量,则两个平面的法向量的夹角即为两平面的二面角或其补角.
试题解析:
解法(1)因为AB=4, BC=CD=2, F是棱AB的中点,
所以BF=BC=CF,△BCF为正三角形, 因为ABCD为
等腰梯形,所以∠BAC=∠ABC=60°,取AF的中点M,
连接DM,则DM⊥AB,所以DM⊥CD,
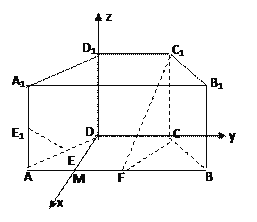
以DM为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,
,则D(0,0,0),A(![]() ,-1,0),F(
,-1,0),F(![]() ,1,0),C(0,2,0),
,1,0),C(0,2,0),
C1(0,2,2),E(![]() ,
,![]() ,0),E1(
,0),E1(![]() ,-1,1),所以
,-1,1),所以
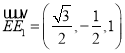 ,
,![]() ,
,![]()
![]()
设平面CC1F的法向量为![]() 则
则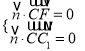 所以
所以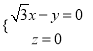 取
取![]() ,则
,则![]() ,所以
,所以![]() ,所以直线EE
,所以直线EE![]() //平面FCC
//平面FCC![]() .
.
(2)![]() ,设平面BFC1的法向量为
,设平面BFC1的法向量为![]() ,则
,则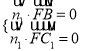 所以
所以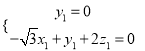 ,取
,取![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
所以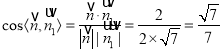 ,由图可知二面角B-FC
,由图可知二面角B-FC![]() -C为锐角,所以二面角B-FC
-C为锐角,所以二面角B-FC![]() -C的余弦值为
-C的余弦值为![]() .
.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目