题目内容
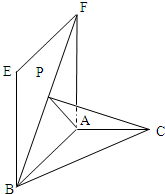 (2008•湖北模拟)如图,直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=2
(2008•湖北模拟)如图,直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=2| 3 |
(1)若PB=PF,求异面直线PC与AB所成的角的余弦值;
(2)若二面角P-AC-B的大小为300,求证:FB⊥平面PAC.
分析:(1)分别取BE、AB的中点M、N,连接PM、MC,PN、NC,则PM=1,MB=
,BC=2
,可得MC=
,又因为PN=MB=
,NC=
,可得PC=2
.进而利用余弦定理求出答案.
(2)连接AP,根据题意可得:∠BAP即为所求二面角的平面角,即∠BAP=30°,进而根据三角形的有关知识可得BF⊥AP,再结合线面垂直可得BF⊥AC,进而根据线面垂直的判定定理证明线面垂直.
| 3 |
| 2 |
| 11 |
| 3 |
| 5 |
| 2 |
(2)连接AP,根据题意可得:∠BAP即为所求二面角的平面角,即∠BAP=30°,进而根据三角形的有关知识可得BF⊥AP,再结合线面垂直可得BF⊥AC,进而根据线面垂直的判定定理证明线面垂直.
解答: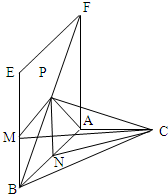 解:(1)分别取BE、AB的中点M、N,
解:(1)分别取BE、AB的中点M、N,
连接PM、MC,PN、NC,则PM=1,MB=
,BC=2
,
∴MC=
,而PN=MB=
,NC=
,
∴PC=2
,…(4分)
∴在△MPC中,由余弦定理可得:cos∠MPC=
=-
故所求PC与AB所成角的余弦值为
…(6分)
(2)连接AP,
∵二面角E-AB-C是直二面角,且AC⊥AB
∴∠BAP即为所求二面角的平面角,即∠BAP=30°…(8分)
在Rt△BAF中,tan∠ABF=
,
∴∠ABF=60°,
故BF⊥AP,…(10分)
又∵AC⊥面BF,
∴BF⊥AC,
又因为AP∩AC=A,并且AP?平面PAC,AC?平面PAC,
所以BF⊥平面PAC…(12分)
 解:(1)分别取BE、AB的中点M、N,
解:(1)分别取BE、AB的中点M、N,连接PM、MC,PN、NC,则PM=1,MB=
| 3 |
| 2 |
∴MC=
| 11 |
| 3 |
| 5 |
∴PC=2
| 2 |
∴在△MPC中,由余弦定理可得:cos∠MPC=
| 1+8-11 | ||
4
|
| ||
| 4 |
故所求PC与AB所成角的余弦值为
| ||
| 4 |
(2)连接AP,
∵二面角E-AB-C是直二面角,且AC⊥AB
∴∠BAP即为所求二面角的平面角,即∠BAP=30°…(8分)
在Rt△BAF中,tan∠ABF=
| 3 |
∴∠ABF=60°,
故BF⊥AP,…(10分)
又∵AC⊥面BF,
∴BF⊥AC,
又因为AP∩AC=A,并且AP?平面PAC,AC?平面PAC,
所以BF⊥平面PAC…(12分)
点评:本题考查利用线面垂直的判定定理证明线面垂直,以及求异面直线所成的角,空间角解决的关键是做角,由图形的结构及题设条件正确作出平面角来,是求角的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 (2008•湖北模拟)已知向量
(2008•湖北模拟)已知向量