题目内容
已知椭圆
+
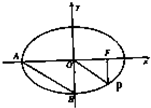
=1(a>b>0),A、B是椭圆上的两点,线段AB的垂直平分线与x轴相交于点P(x0,0).证明-
<x0<
.
| x2 |
| a2 |
| y2 |
| b2 |
| a2-b2 |
| a |
| a2-b2 |
| a |
证明:设A、B的坐标分别为(x1,y1)和(x2,y2).因线段AB的垂直平分线与x轴相交,故AB不平行于y轴,即x1≠x2.又交点为P(x0,0),故|PA|=|PB|,即
(x1-x0)2+y12=(x2-x0)2+y22①
∵A、B在椭圆上,
∴
=b2-
,
=b2-
.
将上式代入①,得
2(x2-x1)x0=(
-
)
②
∵x1≠x2,可得x0=
•
.③
∵-a≤x1≤a,-a≤x2≤a,且x1≠x2,
∴-2a<x1+x2<2a,
∴-
<x0<
.
(x1-x0)2+y12=(x2-x0)2+y22①
∵A、B在椭圆上,
∴
| y | 21 |
| b2 |
| a2 |
| x | 21 |
| y | 22 |
| b2 |
| a2 |
| x | 22 |
将上式代入①,得
2(x2-x1)x0=(
| x | 22 |
| x | 21 |
| a2-b2 |
| a2 |
∵x1≠x2,可得x0=
| x1+x2 |
| 2 |
| a2-b2 |
| a2 |
∵-a≤x1≤a,-a≤x2≤a,且x1≠x2,
∴-2a<x1+x2<2a,
∴-
| a2-b2 |
| a |
| a2-b2 |
| a |

练习册系列答案
相关题目