题目内容
20.设n∈N且n≥15,A,B都是{1,2,3,…,n}真子集,A∩B=∅,且A∪B={1,2,3,…,n}.证明:A或者B中必有两个不同数的和是完全平方数.分析 运用反证法,假设A、B两组中都没有不同的两个数的和是完全平方数,逐步讨论,得出与假设相矛盾的结果.
解答 证明:(反证法)假设A、B中都没有不同的两个数的和是完全平方数.
不妨设1在A中,且n≥15,
由于1+3=22,1+15=42,即3,15都不在A中,
所以3,15都在B中,
又因为3+6=32,即6必不在B中,
即6必须在A,
而6+10=42,即10必须在B中,
这时,B中已有两个数10,15的和为完全平方数了,即10+15=52,
所以,假设不成立,
故在A或B中,必有两个不相同的数的和为完全平方数.
点评 本题主要考查了运用反证法证明集合问题,通过假设反复计算和推理得出A、B两集合中元素的归属,直到得出矛盾,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
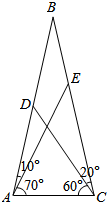 如图,已知∠DAE=10°,∠CAE=70°,∠DCA=60°,∠DCE=20°,则∠DEA=20°.
如图,已知∠DAE=10°,∠CAE=70°,∠DCA=60°,∠DCE=20°,则∠DEA=20°. 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周四尺,高三尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图),米堆底部的弧长为4尺,米堆的高为3尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周四尺,高三尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图),米堆底部的弧长为4尺,米堆的高为3尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有( )