题目内容
12.已知f(x)=2cos(ωx-$\frac{π}{2}$)cos(${ωx+\frac{π}{6}}$)+2sin2ωx-1(ω>0),直线y=$\frac{1}{2}$与f(x)的图象交点之间最短距离为π.(Ⅰ) 求f(x)的解析式及单调递增区间;
(Ⅱ)在△ABC中,角A、B、C所对的边分别是a、b、c若有(2a-c)cosB=bcosC,则求角B的大小以及f(A)的取值范围.
分析 (1)化简得f(x)=$\frac{\sqrt{3}}{2}$sin2ωx-$\frac{1}{2}$cos2ωx-$\frac{1}{2}$=sin(2ωx-$\frac{π}{6}$)-$\frac{1}{2}$,由直线y=$\frac{1}{2}$与f(x)的图象交点之间最短距离为π可知f(x)周期为π,求出ω,结合正弦函数单调性求出
f(x)的单调增区间;
(2)由(2a-c)cosB=bcosC得2sinAcosB-sinCcosB=sinBcosC,整理得cosB=$\frac{1}{2}$,于是B=$\frac{π}{3}$,由A的范围得出2A-$\frac{π}{6}$的范围,从而求出f(A)的范围.
解答 解;(1)f(x)=$\sqrt{3}$sinωxcosωx-sin2ωx+2sin2ωx-1
=$\frac{\sqrt{3}}{2}$sin2ωx-$\frac{1}{2}$cos2ωx-$\frac{1}{2}$=sin(2ωx-$\frac{π}{6}$)-$\frac{1}{2}$,
∵直线y=$\frac{1}{2}$与f(x)的图象交点之间最短距离为π,
∴f(x)的周期T=π,即$\frac{2π}{2ω}$=π,∴ω=1.
∴f(x)=sin(2x-$\frac{π}{6}$)-$\frac{1}{2}$.
令-$\frac{π}{2}$+2kπ≤2x-$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,解得-$\frac{π}{6}$+kπ≤x≤$\frac{π}{3}$+kπ,
∴f(x)的单调递增区间是[-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ],k∈Z.
(2)∵(2a-c)cosB=bcosC,
∴2sinAcosB-sinCcosB=sinBcosC,
即2sinAcosB=sinCcosB+sinBcosC=sin(B+C)=sinA,
∵sinA≠0,∴cosB=$\frac{1}{2}$,∴B=$\frac{π}{3}$.
f(A)=sin(2A-$\frac{π}{6}$)-$\frac{1}{2}$,
∵0<A<$\frac{2π}{3}$.∴$-\frac{π}{6}$<2A-$\frac{π}{6}$<$\frac{7π}{6}$,
∴当2A-$\frac{π}{6}$=$\frac{π}{2}$时,f(A)取得最大值$\frac{1}{2}$,
当2A-$\frac{π}{6}$=-$\frac{π}{6}$或2A-$\frac{π}{6}$=$\frac{7π}{6}$时,f(x)取得最小值-1.
∴f(A)的取值范围是(-1,$\frac{1}{2}$].
点评 本题考查了三角函数的恒等变换和性质,确定A的范围是关键.

| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{7}{2}$ | D. | 1或$\frac{7}{2}$ |
| A. | 1 | B. | -1 | C. | -3 | D. | 3 |
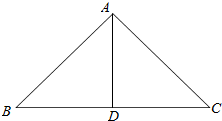 如图:已知△ABC中,∠BAD=∠C,AB=4,BD=2,$\overrightarrow{BD}$=$\overrightarrow{m}$.
如图:已知△ABC中,∠BAD=∠C,AB=4,BD=2,$\overrightarrow{BD}$=$\overrightarrow{m}$.