题目内容

17．$\frac{cos65°-sin80°sin15°}{cos5°-cos10°sin75°}$=2+$\sqrt{3}$．

分析 利用角的等价变换，结合三角函数的公式分别化简求值．

解答 解：原式=$\frac{cos（80°-15°）-sin80°sin15°}{cos（80°-75°）-sin80°sin75°}$=$\frac{cos80°cos15°}{cos80°cos75°}$=$\frac{sin75°}{cos75°}$=tan75°=tan（30°+45°）=$\frac{\frac{\sqrt{3}}{3}+1}{1-\frac{\sqrt{3}}{3}}$=2+$\sqrt{3}$；
故答案为：2+$\sqrt{3}$．

点评 本题考查了三角函数式的化简求值；等积式发现角度之间的关系，进行等价变形，利用三角函数公式化简．

练习册系列答案
相关题目
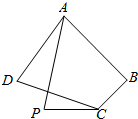7．如图，在四边形ABCD中，AB=AD=4，BC=6，CD=2，3$\overrightarrow{AB}$•$\overrightarrow{AD}$+4$\overrightarrow{CB}$•$\overrightarrow{CD}$=0．
（1）求四边形ABCD的面积；
（2）求三角形ABC的外接圆半径R；
（3）若∠APC=60°，求PA+PC的取值范围．
8．已知1g12=a，lg18=b，试用a，b表示log23．
5．设$\overrightarrow{a}$≠0，$\overrightarrow{b}$≠0，$\overrightarrow{a}$≠$\overrightarrow{b}$，当$\overrightarrow{a}$和$\overrightarrow{b}$满足条件|$\overrightarrow{a}$|=|$\overrightarrow{b}$|时，使得$\overrightarrow{a}$+$\overrightarrow{b}$平分$\overrightarrow{a}$与$\overrightarrow{b}$的夹角．
12．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的焦距为4，左右焦点分别为F1，F2，且经过点（-3，2$\sqrt{6}$）．
（1）求双曲线C的方程；
（2）若P为双曲线上的一点，且|PF1||PF2|=8，求△PF1F2的周长．
2．已知直线l1，l2的斜率k1，k2是关于k的方程2k2-3k-b=0的两根，若l1⊥l2，则b=2；若l1∥l2，则b=-$\frac{9}{8}$．
9．已知直线l1，l2，l3的斜率分别是k1，k2，k3，其中l1∥l2，且k1，k3是方程2x2-3x-2=0的两根，则k1+k2+k3的值是（　　）
A．1B．$\frac{3}{2}$C．$\frac{7}{2}$D．1或$\frac{7}{2}$
6．设函数y=（x+$\sqrt{{x}^{2}+1}$）2，求y′．
20．设n∈N且n≥15，A，B都是{1，2，3，…，n}真子集，A∩B=∅，且A∪B={1，2，3，…，n}．证明：A或者B中必有两个不同数的和是完全平方数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网