题目内容
【题目】已知点
、
的坐标分别是
，
，直线
，
相交于点
，且它们的斜率之积为
.
（1）求动点的轨迹方程；
（2）若过点
的直线
交动点的轨迹于
、
两点， 且
为线段，的中点，求直线的方程.
【答案】（1）
（2）
【解析】
（1）设M（x，y），写出直线AM与直线BM的斜率，利用线AM与直线BM的斜率之积为﹣2，得到x与y的关系，进而得到答案；（2）根据题意可得直线l的斜率存在，设直线l方程和
，
，将C,D坐标代入曲线方程后，利用点差法可得直线l的斜率，从而得到直线方程．
（1）设
，因为
，所以
化简
得：
（2）设，当直线
轴时，直线
的方程为
，则
，
，其中点不是
，不合题意
设直线的方程为
将， 代入得
（1）
（2）
（1）-（2） 整理得：
直线的方程为
即所求直线的方程为
练习册系列答案
相关题目
【题目】假设关于某设备的使用年限
（年）和所支出的维修费用
（万元）有如下统计资料：
| 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
若由资料知， 
对
呈线性相关关系，试求：
（1）回归直线方程；
（2）估计使用年限为10年时，维修费用约是多少？
参考公式：回归直线方程： 
.其中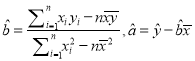
（注： 
)
