题目内容
【题目】设函数f(x)=ax2+bx+c(a,b,c∈R),若x=﹣1为函数y=f(x)ex的一个极值点,则下列图象不可能为y=f(x)的图象是( )
A. 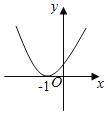 B.
B. 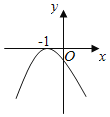
C. 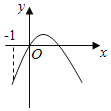 D.
D. 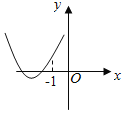
【答案】D
【解析】
先求出函数f(x)ex的导函数,利用x=﹣1为函数f(x)ex的一个极值点可得a,b,c之间的关系,再代入函数f(x)=ax2+bx+c,对答案分别代入验证,看哪个答案不成立即可.
解:由y=f(x)ex=ex(ax2+bx+c)y′=f′(x)ex+exf(x)=ex[ax2+(b+2a)x+b+c],
由x=﹣1为函数f(x)ex的一个极值点可得,﹣1是方程ax2+(b+2a)x+b+c=0的一个根,
所以有a﹣(b+2a)+b+c=0c=a.
法一:所以函数f(x)=ax2+bx+a,对称轴为x![]() ,且f(﹣1)=2a﹣b,f(0)=a.
,且f(﹣1)=2a﹣b,f(0)=a.
对于A,由图得a>0,f(0)>0,f(﹣1)=0,不矛盾,
对于B,由图得a<0,f(0)<0,f(﹣1)=0,不矛盾,
对于C,由图得a<0,f(0)<0,x![]() 0b>0f(﹣1)<0,不矛盾,
0b>0f(﹣1)<0,不矛盾,
对于D,由图得a>0,f(0)>0,x![]() 1b>2af(﹣1)<0与原图中f(﹣1)>0矛盾,D不对.
1b>2af(﹣1)<0与原图中f(﹣1)>0矛盾,D不对.
法二:所以函数f(x)=ax2+bx+a,由此得函数相应方程的两根之积为1,对照四个选项发现,D不成立.
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目