题目内容
若定义在R上的偶函数f(x)满足f(x＋2)＝f(x)，且x∈[0,1]时，f(x)＝x，则方程f(x)＝log3|x|的解有( )
| A．2个 | B．3个 |
| C．4个 | D．多于4个 |
C
若函数f(x)满足f(x＋2)＝f(x)，则函数f(x)是以2为周期的周期函数，又函数是定义在R上的偶函数，结合当x∈[0,1]时，f(x)＝x，在同一坐标系中画出函数y＝f(x)与函数y＝log3|x|的图象如图所示：
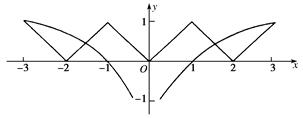
由图可知函数y＝f(x)与函数y＝log3|x|的图象共有4个交点，即方程f(x)＝log3|x|的解的个数是4，故选C.
由图可知函数y＝f(x)与函数y＝log3|x|的图象共有4个交点，即方程f(x)＝log3|x|的解的个数是4，故选C.
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
中，下列描述正确的是（ ）
、值域是R ②图像必过点(1,0).
时，在
时，在
，l1与函数y＝|log2x|的图象从左至右相交于点A、B，l2与函数y＝|log2x|的图象从左至右相交于点C、D.记线段AC和BD在x轴上的投影长度分别为a、b.当m变化时，求
的最小值．
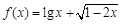的定义域为
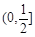
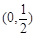
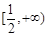
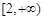
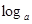(x-1)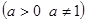
的图象必过定点
, 
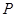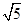＋lg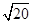
＝________．
.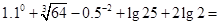