题目内容
已知两条直线l1:y=m和l2:y= ,l1与函数y=|log2x|的图象从左至右相交于点A、B,l2与函数y=|log2x|的图象从左至右相交于点C、D.记线段AC和BD在x轴上的投影长度分别为a、b.当m变化时,求
,l1与函数y=|log2x|的图象从左至右相交于点A、B,l2与函数y=|log2x|的图象从左至右相交于点C、D.记线段AC和BD在x轴上的投影长度分别为a、b.当m变化时,求 的最小值.
的最小值.
 ,l1与函数y=|log2x|的图象从左至右相交于点A、B,l2与函数y=|log2x|的图象从左至右相交于点C、D.记线段AC和BD在x轴上的投影长度分别为a、b.当m变化时,求
,l1与函数y=|log2x|的图象从左至右相交于点A、B,l2与函数y=|log2x|的图象从左至右相交于点C、D.记线段AC和BD在x轴上的投影长度分别为a、b.当m变化时,求 的最小值.
的最小值.8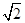
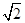
由题意得xA=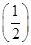 m,xB=2m,xC=
m,xB=2m,xC=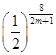 ,xD=
,xD=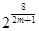 ,所以a=|xA-xC|=
,所以a=|xA-xC|=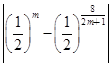 ,b=|xB-xD|=
,b=|xB-xD|=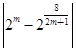 ,即
,即 =
=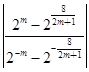 =
=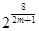 ·2m=2
·2m=2 +m.
+m.
因为 +m=
+m=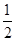 (2m+1)+
(2m+1)+ -
-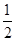 ≥2
≥2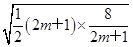 -
-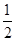 =
=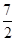 ,当且仅当
,当且仅当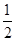 (2m+1)=
(2m+1)=
 ,即m=
,即m=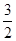 时取等号.所以,
时取等号.所以, 的最小值为
的最小值为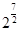 =8
=8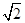 .
.
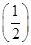 m,xB=2m,xC=
m,xB=2m,xC=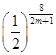 ,xD=
,xD=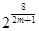 ,所以a=|xA-xC|=
,所以a=|xA-xC|=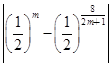 ,b=|xB-xD|=
,b=|xB-xD|=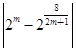 ,即
,即 =
=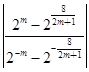 =
=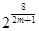 ·2m=2
·2m=2 +m.
+m.因为
 +m=
+m=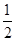 (2m+1)+
(2m+1)+ -
-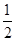 ≥2
≥2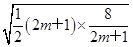 -
-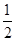 =
=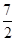 ,当且仅当
,当且仅当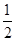 (2m+1)=
(2m+1)= ,即m=
,即m=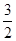 时取等号.所以,
时取等号.所以, 的最小值为
的最小值为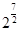 =8
=8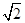 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的解是 .
的解是 . =4,则f(2 014)的值为________.
=4,则f(2 014)的值为________. ,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.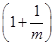 +loga
+loga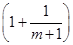 +…+loga
+…+loga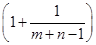 =logam+logan,求m、n的值.
=logam+logan,求m、n的值. 的值是____________.
的值是____________.