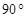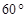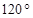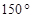题目内容
已知函数f(x)=log4(4x+1)+kx(k∈R)为偶函数.
(1)求k的值;
(2)若方程f(x)=log4(a·2x-a)有且只有一个根,求实数a的取值范围.
(1)求k的值;
(2)若方程f(x)=log4(a·2x-a)有且只有一个根,求实数a的取值范围.
(1)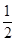 (2) a的取值范围为{a|a>1或a=-2-2
(2) a的取值范围为{a|a>1或a=-2-2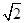 }
}
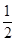 (2) a的取值范围为{a|a>1或a=-2-2
(2) a的取值范围为{a|a>1或a=-2-2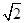 }
}解:(1)∵f(x)为偶函数,∴f(-x)=f(x),
即log4(4-x+1)-kx=log4(4x+1)+kx,
即(2k+1)x=0,∴k=-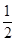 .
.
(2)依题意令log4(4x+1)-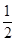 x=log4 (a·2x-a),
x=log4 (a·2x-a),
即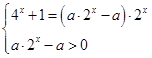
令t=2x,则(1-a)t2+at+1=0,只需其有一正根即可满足题意.
①当a=1时,t=-1,不合题意,舍去.
②上式有一正一负根t1,t2,
即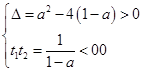
经验证满足a·2x-a>0,∴a>1.
③上式有两根相等,即Δ=0⇒a=±2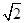 -2,此时t=
-2,此时t=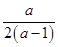 ,若a=2(
,若a=2(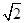 -1),则有t=
-1),则有t=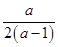 <0,此时方程(1-a)t2+at+1=0无正根,故a=2(
<0,此时方程(1-a)t2+at+1=0无正根,故a=2(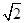 -1)舍去;
-1)舍去;
若a=-2(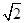 +1),则有t=
+1),则有t=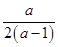 >0,且a· 2x-a=a(t-1)=a
>0,且a· 2x-a=a(t-1)=a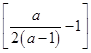 =
=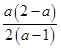 >0,因此a=-2(
>0,因此a=-2(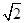 +1).
+1).
综上所述,a的取值范围为{a|a>1或a=-2-2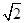 }.
}.
即log4(4-x+1)-kx=log4(4x+1)+kx,
即(2k+1)x=0,∴k=-
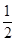 .
.(2)依题意令log4(4x+1)-
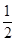 x=log4 (a·2x-a),
x=log4 (a·2x-a),即
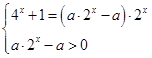
令t=2x,则(1-a)t2+at+1=0,只需其有一正根即可满足题意.
①当a=1时,t=-1,不合题意,舍去.
②上式有一正一负根t1,t2,
即
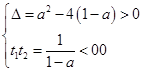
经验证满足a·2x-a>0,∴a>1.
③上式有两根相等,即Δ=0⇒a=±2
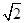 -2,此时t=
-2,此时t=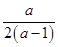 ,若a=2(
,若a=2(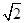 -1),则有t=
-1),则有t=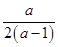 <0,此时方程(1-a)t2+at+1=0无正根,故a=2(
<0,此时方程(1-a)t2+at+1=0无正根,故a=2(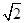 -1)舍去;
-1)舍去;若a=-2(
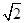 +1),则有t=
+1),则有t=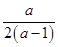 >0,且a· 2x-a=a(t-1)=a
>0,且a· 2x-a=a(t-1)=a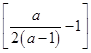 =
=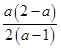 >0,因此a=-2(
>0,因此a=-2(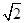 +1).
+1).综上所述,a的取值范围为{a|a>1或a=-2-2
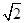 }.
}.
练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目
 的解是 .
的解是 . .
. )+f(-
)+f(- )
) ,若f(a)+f(b)=0,且0<a<b<1,则ab的取值范围是________.
,若f(a)+f(b)=0,且0<a<b<1,则ab的取值范围是________.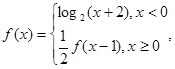 若函数
若函数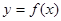 与
与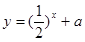 的图象有三个不同交点,则实数
的图象有三个不同交点,则实数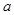 的取值范围是 .
的取值范围是 .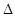 ABC中,若
ABC中,若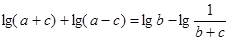 ,则A=( )
,则A=( )