Question

12．如图，过抛物线y²=2px（p＞0）的焦点F的直线l交抛物线于点A，B，交其准线于点C，若|BC|=2|BF|，且|AF|=3，求此抛物线的方程．

Answer 1

分析 根据过抛物线y²=2px（p＞0）的焦点F的直线l交抛物线于点A、B，作AM、BN垂直准线于点M、N，根据|BC|=2|BF|，且|AF|=3，和抛物线的定义，可得∠NCB=30°，设A（x₁，y₁），B（x₂，y₂），|BF|=x，而x₁+$\frac{p}{2}$=3，x₂+$\frac{p}{2}$=1，且x₁x₂=$\frac{{p}^{2}}{4}$，可求得p的值，即求得抛物线的方程．

解答 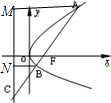解：设A（x₁，y₁），B（x₂，y₂），
过焦点F（$\frac{p}{2}$，0）的直线l设为y=k（x-$\frac{p}{2}$），
代入抛物线方程，可得k²x²-p（k²+2）x+$\frac{{k}^{2}{p}^{2}}{4}$=0，
x₁x₂=$\frac{{p}^{2}}{4}$．
k不存在，上式显然成立．
作AM、BN垂直准线于点M、N，
则|BN|=|BF|，
又|BC|=2|BF|，得|BC|=2|BN|，
∴∠NCB=30°，
有|AC|=2|AM|=6，
设|BF|=x，则2x+x+3=6⇒x=1，
而x₁+$\frac{p}{2}$=3，x₂+$\frac{p}{2}$=1，且x₁x₂=$\frac{{p}^{2}}{4}$，
∴（3-$\frac{p}{2}$）（1-$\frac{p}{2}$）=$\frac{{p}^{2}}{4}$，解得p=$\frac{3}{2}$．
即有抛物线的标准方程为y²=3x．

点评 此题是个中档题．考查抛物线的定义以及待定系数法求抛物线的标准方程．体现了数形结合的思想，特别是解析几何，一定要注意对几何图形的研究，以便简化计算．