题目内容
3.已知各项均不相等的等差数列{an}的前四项和S4=14,且a1,a3,a7成等比.(1)求数列{an}的通项公式;
(2)设Tn为数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和,若Tn≤λan+1对一切n∈N*恒成立,求实数λ的最小值.
分析 (1)通过解方程组$\left\{\begin{array}{l}{4{a}_{1}+6d=14}\\{({a}_{1}+2d)^{2}={a}_{1}•({a}_{1}+6d)}\end{array}\right.$,进而计算可得结论;
(2)通过(1)、裂项可知$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{n+1}$-$\frac{1}{n+2}$,进而并项相加可知Tn=$\frac{n}{2(n+2)}$,通过变形可知问题转化为求$\frac{1}{2}$•$\frac{1}{4+(n+\frac{4}{n})}$的最大值,进而计算可得结论.
解答 解:(1)由题意,$\left\{\begin{array}{l}{4{a}_{1}+6d=14}\\{({a}_{1}+2d)^{2}={a}_{1}•({a}_{1}+6d)}\end{array}\right.$,
解得:a1=2,d=1,
∴数列{an}的通项公式an=a1+(n-1)d=n+1;
(2)由(1)知:an=n+1,
∴$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(n+1)(n+2)}$=$\frac{1}{n+1}$-$\frac{1}{n+2}$,
∴Tn=$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n+1}$-$\frac{1}{n+2}$=$\frac{1}{2}$-$\frac{1}{n+2}$=$\frac{n}{2(n+2)}$,
∵Tn≤λan+1对一切n∈N*恒成立,
∴λ≥$\frac{{T}_{n}}{{a}_{n+1}}$=$\frac{\frac{n}{2(n+2)}}{n+2}$=$\frac{1}{2}$•$\frac{1}{4+(n+\frac{4}{n})}$对一切n∈N*恒成立,
又∵n+$\frac{4}{n}$≥2$\sqrt{n•\frac{4}{n}}$=4,当且仅当n=$\frac{4}{n}$即n=2时取等号,
∴$\frac{1}{2}$•$\frac{1}{4+(n+\frac{4}{n})}$≤$\frac{1}{2}•\frac{1}{4+4}$=$\frac{1}{16}$,
∴实数λ的最小值为$\frac{1}{16}$.
点评 本题考查的数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 100和0.8 | B. | 20和0.4 | C. | 10和0.8 | D. | 10和0.2 |
| A. | a-3<b-3 | B. | -3a<-3b | C. | a2<b2 | D. | $\frac{1}{a}$$<\frac{1}{b}$ |
(1)作出散点图,并求出回归直线方程;
(2)根据(1)中求出的回归直线方程,预测生产A产品10(吨)时相应的生产能耗为多少(吨)?
| X | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 6 |
Sn2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]
公式组Ⅱ.$\widehat{y}$=$\widehat{b}$x+$\widehat{a}•\widehat{b}$=$\frac{\sum_{i+1}^{n}{x}_{1}{y}_{1}-n\overline{x}\overline{y}}{\sum_{i+1}^{n}{x}_{1}^{2}-n{\overline{x}}^{2}}$)
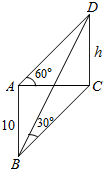 一个人在建筑物的正西A点,测得建筑物顶的仰角是60°,这个人再从A点向南走到B点,再测得建筑物顶的仰角是30°,设A、B间的距离是10米,求建筑物的高.
一个人在建筑物的正西A点,测得建筑物顶的仰角是60°,这个人再从A点向南走到B点,再测得建筑物顶的仰角是30°,设A、B间的距离是10米,求建筑物的高. 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A,B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,求此抛物线的方程.
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A,B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,求此抛物线的方程.