题目内容
10.数列{an}满足 a1=3,an+1=$\frac{2}{{a}_{n}+1}$.(1)求证:{$\frac{{a}_{n}-1}{{a}_{n}+2}$}成等比数列;
(2)若an-t2-mt≥0对一切n∈N*及m∈[-1,1]恒成立,求实数t的取值范围.
分析 (1)通过an+1=$\frac{2}{{a}_{n}+1}$,计算出an+1-1=$\frac{1-{a}_{n}}{1+{a}_{n}}$、an+1+2=$\frac{4+2{a}_{n}}{1+{a}_{n}}$,作商即得结论;
(2)通过(1)知Qn=$\frac{{a}_{n}-1}{{a}_{n}+2}$=$\frac{2}{5}$•(-$\frac{1}{2}$)n-1,从而通过Qn∈[-$\frac{1}{5}$,$\frac{2}{5}$]可得an∈[$\frac{1}{2}$,3],则原条件即转化为为:-t2-mt+$\frac{1}{2}$≥0对一切n∈N*及m∈[-1,1]恒成立,进而有t∈[-$\frac{m+\sqrt{2+{m}^{2}}}{2}$,$\frac{\sqrt{2+{m}^{2}}-m}{2}$],当m∈[-1,1]时,讨论$\frac{\sqrt{2+{m}^{2}}-m}{2}$的最小值、-$\frac{m+\sqrt{2+{m}^{2}}}{2}$的最大值即可.
解答 (1)证明:∵an+1=$\frac{2}{{a}_{n}+1}$,
∴an+1-1=$\frac{2}{{a}_{n}+1}$-1=$\frac{1-{a}_{n}}{1+{a}_{n}}$,
an+1+2=$\frac{2}{{a}_{n}+1}$+2=$\frac{4+2{a}_{n}}{1+{a}_{n}}$,
∴$\frac{{a}_{n+1}-1}{{a}_{n+1}+2}$=$\frac{\frac{1-{a}_{n}}{1+{a}_{n}}}{\frac{4+2{a}_{n}}{1+{a}_{n}}}$=-$\frac{1}{2}$•$\frac{{a}_{n}-1}{{a}_{n}+2}$,
∴数列{$\frac{{a}_{n}-1}{{a}_{n}+2}$}成公比为-$\frac{1}{2}$的等比数列;
(2)解:由(1)知数列{$\frac{{a}_{n}-1}{{a}_{n}+2}$}的公比为-$\frac{1}{2}$,
∵a1=3,
∴$\frac{{a}_{1}-1}{{a}_{1}+2}$=$\frac{3-1}{3+2}$=$\frac{2}{5}$,
∴$\frac{{a}_{n}-1}{{a}_{n}+2}$=1-$\frac{3}{{a}_{n}+2}$=$\frac{2}{5}$•(-$\frac{1}{2}$)n-1,
记Qn=$\frac{{a}_{n}-1}{{a}_{n}+2}$=$\frac{2}{5}$•(-$\frac{1}{2}$)n-1,则Qn∈[-$\frac{1}{5}$,$\frac{2}{5}$],
∴1-Qn∈[$\frac{3}{5}$,$\frac{6}{5}$],
∴$\frac{1}{1-{Q}_{n}}$∈[$\frac{5}{6}$,$\frac{5}{3}$],
∴an=$\frac{3}{1-{Q}_{n}}$-2∈[$\frac{1}{2}$,3],
∴an-t2-mt≥0对一切n∈N*及m∈[-1,1]恒成立,
等价于:-t2-mt+$\frac{1}{2}$≥0对一切n∈N*及m∈[-1,1]恒成立,
令t2+mt-$\frac{1}{2}$=0,
解得:t=$\frac{-m±\sqrt{{m}^{2}+2}}{2}$,
则-t2-mt+$\frac{1}{2}$≥0的解集为:t∈[-$\frac{m+\sqrt{2+{m}^{2}}}{2}$,$\frac{\sqrt{2+{m}^{2}}-m}{2}$],
当m∈[-1,1]时,$\frac{\sqrt{2+{m}^{2}}-m}{2}$的最小值为$\frac{\sqrt{3}-1}{2}$,
-$\frac{m+\sqrt{2+{m}^{2}}}{2}$的最大值为$\frac{1-\sqrt{3}}{2}$,
∴实数t的取值范围为:[$\frac{1-\sqrt{3}}{2}$,$\frac{\sqrt{3}-1}{2}$].
点评 本题是一道关于数列与函数的综合题,考查判定数列为等比数列,考查解一元二次不等式,考查运算求解能力,注意解题方法的积累,属于难题.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案| A. | 150° | B. | 120° | C. | 60° | D. | 75° |
| A. | 命题“若xy=0,则x=0或y=0”的否命题为“若xy≠0,则x≠0或y≠0” | |
| B. | 若命题p为假命题,命题¬q为真命题,则命题“p∨q”为真命题 | |
| C. | “$\frac{a}{b}$>1”是“a>b>0”的必要不充分条件 | |
| D. | 命题“任意x>1,x+1>2”的否定是“存在x≤1,x+1≤2” |
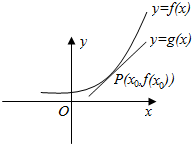 已知可导函数y=f(x)在点P(x0,f(x0))处切线为l:y=g(x)(如图),设F(x)=f(x)-g(x),则( )
已知可导函数y=f(x)在点P(x0,f(x0))处切线为l:y=g(x)(如图),设F(x)=f(x)-g(x),则( )| A. | F′(x0)=0,x=x0是F(x)的极大值点 | B. | F′(x0)=0,x=x0是F(x)的极小值点 | ||
| C. | F′(x0)≠0,x=x0不是F(x)的极值点 | D. | F′(x0)≠0,x=x0是F(x)的极值点 |
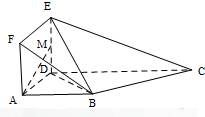 如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD为直角梯形,且AB∥CD,AB⊥AD,AB=AD=$\frac{1}{2}$CD=1,M为线段ED上的动点.
如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD为直角梯形,且AB∥CD,AB⊥AD,AB=AD=$\frac{1}{2}$CD=1,M为线段ED上的动点.