题目内容
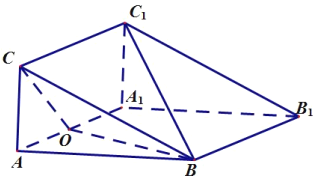
【题目】如图,在多面体![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,四边形
,四边形![]() 是矩形,
是矩形,![]() 和
和![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,
,![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)见解析.
(2) ![]() .
.
【解析】分析:(1)连接![]() 交
交![]() 于点
于点![]() ,由三角形中位线定理可得
,由三角形中位线定理可得![]() ,由线面平行的判定定理可得
,由线面平行的判定定理可得![]() 平面
平面![]() ,同理
,同理![]() 平面
平面![]() ,从而可得结论;(2)过点
,从而可得结论;(2)过点![]() 在平面
在平面![]() 中作
中作![]() 轴
轴![]() ,以
,以![]() 为
为![]() 轴,建立空间直角坐标系,分别利用向量垂直数量积为零列方程组,求出. 平面
轴,建立空间直角坐标系,分别利用向量垂直数量积为零列方程组,求出. 平面![]() 与平面
与平面![]() 法向量,由空间向量夹角余弦公式可得结果.
法向量,由空间向量夹角余弦公式可得结果.
详解:(1)连接![]() 交
交![]() 于点
于点![]() ,显然
,显然![]() ,
,![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,可得
,可得![]() 平面
平面![]() ,同理
,同理![]() 平面
平面![]() ,
,![]() , 又
, 又![]() 平面
平面![]() ,可得:平面
,可得:平面![]() 平面
平面![]() .
.
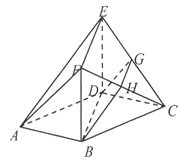
(2)过点![]() 在平面
在平面![]() 中作
中作![]() 轴
轴![]() ,显然
,显然![]() 轴、
轴、![]() 、
、![]() 两两垂直,如图所示建立空间直角坐标系.
两两垂直,如图所示建立空间直角坐标系.![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .设平面
.设平面![]() 与平面
与平面![]() 法向量分别为
法向量分别为![]() ,
,![]() .
.
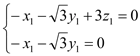 ,设
,设![]() ;
;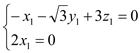 ,设
,设![]() .
.
![]() ,综上:面
,综上:面![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.

【题目】为建立健全国家学生体质健康监测评价机制,激励学生积极参加身体锻炼,教育部印发《国家学生体质健康标准(2014年修订)》,要求各学校每学期开展覆盖本校各年级学生的《标准》测试工作,并根据学生每个学期总分评定等级.某校决定针对高中学生,每学期进行一次体质健康测试,以下是小明同学六个学期体质健康测试的总分情况.
学期 | 1 | 2 | 3 | 4 | 5 | 6 |
总分 | 512 | 518 | 523 | 528 | 534 | 535 |
(1)请根据上表提供的数据,用相关系数![]() 说明
说明![]() 与
与![]() 的线性相关程度,并用最小二乘法求出
的线性相关程度,并用最小二乘法求出![]() 关于
关于![]() 的线性回归方程(线性相关系数保留两位小数);
的线性回归方程(线性相关系数保留两位小数);
(2)在第六个学期测试中学校根据 《标准》,划定540分以上为优秀等级,已知小明所在的学习小组10个同学有6个被评定为优秀,测试后同学们都知道了自己的总分但不知道别人的总分,小明随机的给小组内4个同学打电话询问对方成绩,优秀的同学有![]() 人,求
人,求![]() 的分布列和期望.
的分布列和期望.
参考公式: 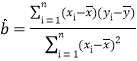 ,
,![]() ;
;
相关系数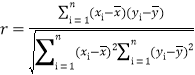 ;
;
参考数据:![]() ,
,![]() .
.