Question

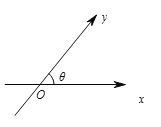
【题目】如图，数轴，的交点为，夹角为，与轴、轴正向同向的单位向量分别是，.由平面向量基本定理，对于平面内的任一向量，存在唯一的有序实数对，使得，我们把叫做点在斜坐标系中的坐标（以下各点的坐标都指在斜坐标系中的坐标）.

（1）若，为单位向量，且与的夹角为，求点的坐标；

（2）若，点的坐标为，求向量与的夹角；

（3）若，求过点的直线的方程，使得原点到直线的距离最大.

Answer 1

【答案】（1）

（2）

（3）

【解析】

（1）设出P点的坐标，结合为单位向量，且与的夹角为，列式求解；

（2）由题意求出，代入数量积求夹角公式得答案.

（3）由题意得到A在直角坐标系和斜坐标系下坐标的关系，求出直角坐标系下使得原点O到直线l的距离最大的直线方程，转化为斜坐标系下的方程，即得解.

（1）若，为单位向量，且与的夹角为，

设，且

代入，得

（2）若，点的坐标为，则

又

设向量与的夹角为，则

（3）若，点

由，可得A在直角坐标系下得坐标为：

因此过点且使得原点O到直线l的距离最大的直线方程为：

代入：

整理得：

所以过点的直线的方程，使得原点到直线的距离最大的直线方程为：