题目内容
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数,
为自然对数的底数,![]() 。
。
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 的值;
的值;
(Ⅱ)若![]() ,问函数
,问函数![]() 有无极值点?若有,请求出极值点的个数;若没有,请说明理由。
有无极值点?若有,请求出极值点的个数;若没有,请说明理由。
【答案】(Ⅰ)a=1;(Ⅱ)答案见解析.
【解析】
(Ⅰ)由题意可得f′(x)=aex+(ax1)ex+a,利用导函数研究函数的切线方程确定实数a的值即可;
(Ⅱ)当![]() 时,
时,![]() ,∴
,∴![]() ,
,
设g(x)=ex(x1)+1,则g′(x)=xex,据此可确定![]() 的符号,从而确定函数
的符号,从而确定函数![]() 有无极值点.
有无极值点.
(Ⅰ)由题意得f(x)=(ax1)ex+ax+1,
∴f′(x)=aex+(ax1)ex+a,
∵在点(0,f(0))处的切线与直线xy+1=0平行,
∴切线的斜率为f′(0)=a1+a=1,解得a=1.
(Ⅱ)当![]() 时,
时,![]() ,
,
∴![]() ,
,
设g(x)=ex(x1)+1,则g′(x)=ex(x1)+ex=xex,
则函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
函数![]() ,
,
据此可得![]() 恒成立,
恒成立,
函数![]() 在定义域内单调递增,函数不存在极值点.
在定义域内单调递增,函数不存在极值点.

 阅读快车系列答案
阅读快车系列答案【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
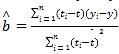 ,
,![]()
【题目】如图所示的数表为“森德拉姆筛”(森德拉姆,东印度学者),其特点是每行每列都成等差数列.在此表中,数字“121”出现的次数为___________.
2 | 3 | 4 | 5 | 6 | 7 | …… |
3 | 5 | 7 | 9 | 11 | 13 | …… |
4 | 7 | 10 | 13 | 16 | 19 | …… |
5 | 9 | 13 | 17 | 21 | 25 | …… |
6 | 11 | 16 | 21 | 26 | 31 | …… |
7 | 13 | 19 | 25 | 31 | 37 | …… |
…… | …… | …… | …… | …… | …… | …… |