题目内容
【题目】已知函数f(x)=Asin(ωx+φ)(A,ω>0,﹣π<φ<π)在一个周期内的图象如图所示. 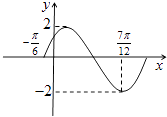
(1)求f(x)的表达式;
(2)在△ABC中,f(C+ ![]() )=﹣1且
)=﹣1且 ![]() <0,求角C.
<0,求角C.
【答案】
(1)解:由图可知函数的最大值是2,最小值是﹣2,
∴A=2,
∵ ![]() T=
T= ![]() +
+ ![]() =
= ![]() ,
,
∴T=π= ![]() ,可得:ω=2,
,可得:ω=2,
又∵f(x)过点(﹣ ![]() ,0),且根据图象特征得:﹣2×
,0),且根据图象特征得:﹣2× ![]() +φ=0+2kπ,k∈Z,
+φ=0+2kπ,k∈Z,
∴φ= ![]() +2kπ,k∈Z,
+2kπ,k∈Z,
而﹣π<φ<π,
∴φ= ![]() .
.
∴f(x)=2sin(2x+ ![]() )
)
(2)解:∵f(x)=2sin(2x+ ![]() ),
),
∴f(C+ ![]() )=2sin(2C
)=2sin(2C ![]() )=﹣1,
)=﹣1,
∴sin(2C ![]() )=﹣
)=﹣ ![]() ,
,
因为C为三角形内角,
∴C= ![]() 或
或 ![]() ,
,
又∵ ![]() =abcosC<0,0<C<π,
=abcosC<0,0<C<π,
∴cosC<0, ![]() <C<π,
<C<π,
∴C= ![]()
【解析】(1)由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,从而求得函数f(x)的表达式.(2)利用(1)及f(C+ ![]() )=﹣1可得sin(2C
)=﹣1可得sin(2C ![]() )=﹣
)=﹣ ![]() ,结合角的范围可求C=
,结合角的范围可求C= ![]() 或
或 ![]() ,利用平面向量数量积的运算可求cosC<0,从而可求C的值.
,利用平面向量数量积的运算可求cosC<0,从而可求C的值.

练习册系列答案
相关题目