Question

【题目】如图所示，四棱锥P﹣ABCD的底面是边长为2的正方形，平面PAD⊥平面ABCD，PA⊥AD，∠PDA＝45°，E，F分别为AB，PC的中点.

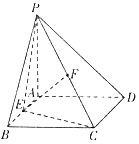
（1）证明：EF∥平面PAD；

（2）在线段BC上是否存在一点H，使平面PAH⊥平面DEF？若存在，求此时二面角C﹣HD﹣P的平面角的正切值：若不存在，说明理由.

Answer 1

【答案】（1）证明见解析（2）存在，正切值为

【解析】

（1）取中点，连接，，则是的中位线，推导出是平行四边形，从而，由此能证明平面；

（2）当为中点时，，推导出平面，平面平面，过点作于点，则为二面角的平面角的补角，由此能求出二面角的平面角的正切值.

（1）证明：取PD中点M，连结AM，FM，

则MF是△PCD的中位线，

∴MF∥CD，且MF，

又四边形ABCD是正方形，则AE∥CD，

且E为AB中点，则AEABCD，

∴AE∥MF，且AE＝MF，∴AMFE是平行四边形，

∴EF∥AM，

又AM平面PAD，EF平面PAD，

∴EF∥平面PAD.

（2）解：在正方形中，取H为BC中点，为的中点，易证ED⊥AH，

又∵AP⊥ED，且AP，AH为平面APH内两相交直线，

∴ED⊥平面PAH，

又ED平面DEF，∴平面EFD⊥平面PAH，

此时，过点A作AG⊥DH于点G，

则∠PGA为二面角C﹣HD﹣P的平面角的补角，

由，则AG，tan∠AGP，

∴二面角C﹣HD﹣P的平面角的正切值为.