题目内容
【题目】已知集合M=![]() ,对它的非空子集A,可将A中每个元素K都乘以
,对它的非空子集A,可将A中每个元素K都乘以![]() 再求和(如A=
再求和(如A=![]() ,可求得和为
,可求得和为![]() ),则对M的所有非空子集,这些和的总和是__________________.
),则对M的所有非空子集,这些和的总和是__________________.
【答案】96
【解析】
根据题意,将M中所有非空子集按元素个数分类考虑,先将所有非空子集中含有1的子集总数确定,同理确定含有2,3,4,5,6的总个数,再按给定的定义求解.
因为集合M=![]() ,
,
所以M的所有非空子集中含1的共有6类:
单元素集合,只有{1},即1出现了![]() 次,
次,
双元素集合,有{1,2},{1,3},{1,4},{1,5},{1,6},即1出现了![]() 次,
次,
三元素集合,有{1,2,3},{1,2,4},{1,2,5},{1,2,6}
{1,3,4},{1,3,5},{1,3,6},
{1,4,5},{1,4,6}
{1,5,6},即1出现了![]() 次,
次,
…
依此推,
含有6个元素的有{1,2,3,4,5,6},即1出现了![]() 次,
次,
所以1共出现![]() 次.
次.
同理2,3,4,5,6各出现![]() 次,
次,
所以M的所有非空子集,这些和的总和是![]() .
.
故答案为:96

练习册系列答案
相关题目
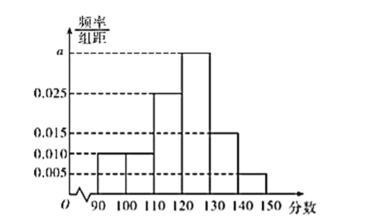
【题目】某高校在2012年的自主招生考试成绩中随机抽取![]() 名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| ① |
|
第3组 |
| 30 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|

(1)请先求出频率分布表中![]() 位置的相应数据,再完成频率分布直方图;
位置的相应数据,再完成频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第![]() 组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,学校决定在![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受
名学生接受![]() 考官进行面试,求:第
考官进行面试,求:第![]() 组至少有一名学生被考官
组至少有一名学生被考官![]() 面试的概率.
面试的概率.