题目内容
已知公差不为0的等差数列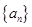 满足
满足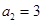 ,
,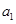 ,
,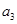 ,
,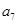 成等比数列.
成等比数列.
(1)求数列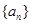 的通项公式;(2)数列
的通项公式;(2)数列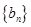 满足
满足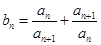 ,求数列
,求数列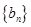 的前
的前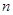 项和
项和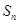 ;(Ⅲ)设
;(Ⅲ)设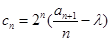 ,若数列
,若数列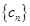 是单调递减数列,求实数
是单调递减数列,求实数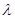 的取值范围.
的取值范围.
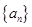 满足
满足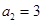 ,
,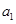 ,
,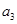 ,
,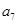 成等比数列.
成等比数列. (1)求数列
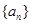 的通项公式;(2)数列
的通项公式;(2)数列 满足
满足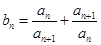 ,求数列
,求数列 的前
的前 项和
项和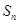 ;(Ⅲ)设
;(Ⅲ)设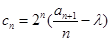 ,若数列
,若数列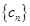 是单调递减数列,求实数
是单调递减数列,求实数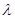 的取值范围.
的取值范围.(1) ;(2)
;(2) ;(3)
;(3) .
.
 ;(2)
;(2) ;(3)
;(3) .
.试题分析:(1)由等差数列的通项公式可将条件
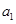 ,
,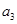 ,
,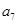 成等比数列,转化为关于公差的方程,解此方程求得公差值,从而就可写出其通项公式;(2)由(1)的结果可求得数列
成等比数列,转化为关于公差的方程,解此方程求得公差值,从而就可写出其通项公式;(2)由(1)的结果可求得数列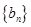 的通项公式,发现其前n项和可用裂项相消求和法解决;(3)数列
的通项公式,发现其前n项和可用裂项相消求和法解决;(3)数列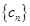 是单调递减数列,等价于
是单调递减数列,等价于 对
对 都成立,将(1)的结果代入,然后将参数
都成立,将(1)的结果代入,然后将参数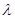 分离出来,可转化为研究一个新数列的最大项问题,对此新数列再用比差法研究其单调性,进而就可求得其最大项,从而获得
分离出来,可转化为研究一个新数列的最大项问题,对此新数列再用比差法研究其单调性,进而就可求得其最大项,从而获得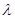 的取值范围.
的取值范围.试题解析:(1)由题知
 ,设
,设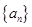 的公差为
的公差为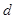 ,则
,则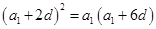 ,
, ,
,

 .
. 
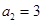



 .
.(2)
 .
. 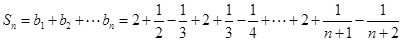
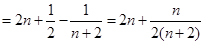 .
. (3)
 ,使数列
,使数列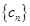 是单调递减数列,
是单调递减数列,则
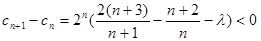 对
对 都成立
都成立 即

设




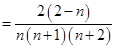

当
 或
或 时,
时, 所以
所以 所以
所以 .
. 
练习册系列答案
相关题目
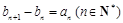 ,b1 = 3,求数列
,b1 = 3,求数列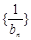 的前n项和Tn.
的前n项和Tn.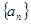 满足
满足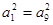 ,则数列
,则数列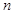 项和
项和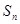 取最大值时,
取最大值时,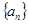 为等差数列,若
为等差数列,若 ,且它们的前n项和
,且它们的前n项和 有最大值,
有最大值, 的n的最大值为( ).
的n的最大值为( ).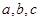 成等差数列,
成等差数列,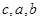 成等比数列,且
成等比数列,且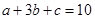 ,则
,则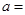
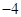
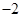
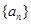 的前n项和
的前n项和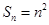 ,则
,则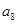 的值为( ).
的值为( ).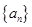 ,
,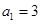 ,
,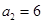 ,且
,且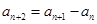 ,则数列的第五项为( )
,则数列的第五项为( )



 满足
满足 ,
,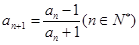 ,则
,则 ( )
( )


 的前
的前 项和为
项和为 ,且
,且 ,则
,则 ______.
______.