题目内容
12.设等比数列{an}的首项a1=$\frac{1}{3}$,前n项和为Sn,若S1、2S2、3S3成等差数列,则{an}的通项为( )| A. | an=$\frac{1}{{3}^{n}}$ | B. | an=3n | C. | an=$\frac{1}{{3}^{n-1}}$ | D. | an=$\frac{1}{{3}^{1-n}}$ |
分析 设等比数列{an}的公比为q,运用等差数列的性质和等比数列的通项公式,解方程可得公比q,再由等比数列的通项公式即可得到.
解答 解:设等比数列{an}的公比为q,
若S1、2S2、3S3成等差数列,
则4S2=S1+3S3,
即为4(a1+a1q)=a1+3(a1+a1q+a1q2),
即有4+4q=4+3q+3q2,
解得q=$\frac{1}{3}$,
即有an=a1qn-1=$\frac{1}{3}•$($\frac{1}{3}$)n-1=$\frac{1}{{3}^{n}}$.
故选A.
点评 本题考查等比数列的通项公式和等差数列的性质,考查化简的运算能力,属于基础题.

练习册系列答案
相关题目
2.阅读如图所示的程序框图,则该算法最后输出的结果为( )
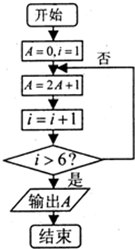

| A. | 15 | B. | 31 | C. | 63 | D. | 127 |
 如图是正方体的平面展开图,则在这个正方体中,求证:DE∥平面BCM.
如图是正方体的平面展开图,则在这个正方体中,求证:DE∥平面BCM.