题目内容
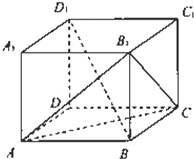 如图,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,BB=
如图,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,BB=| 2 |
(1)求证:BD1⊥AC;
(2)求点C1到平面AB1C的距离.
分析:(Ⅰ)利用正方形的性质、线面垂直的判定和性质定理即可得出;
(Ⅱ)利用“等积变形”即可求出.
(Ⅱ)利用“等积变形”即可求出.
解答:(Ⅰ)证明:连接DB,由长方体知DD1⊥面ABCD,
∴AC⊥DD1,
又ABCD为正方形,∴AC⊥BD,
又DD1∩BD=D,
∴AC⊥面DD1B,BD1?面DDB1,
∴BD1⊥AC.
(Ⅱ)设点C1到面AB1C的距离为h.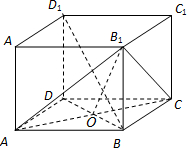
由VC1-AB1C=VA-B1C1C得
S△AB1C•h=
S△B1C1C•AB,
设AC与BD的交点为O,连接B1O,则AC⊥OB1.
∵B1A=B1C=
=
,AC=2
,∴OB1=
=2.
∴S△AB1C=
×2
×2=2
.
而S△B1C1C=
×2×
=
,
∴h=
=
=1.
∴AC⊥DD1,
又ABCD为正方形,∴AC⊥BD,
又DD1∩BD=D,
∴AC⊥面DD1B,BD1?面DDB1,
∴BD1⊥AC.
(Ⅱ)设点C1到面AB1C的距离为h.

由VC1-AB1C=VA-B1C1C得
| 1 |
| 3 |
| 1 |
| 3 |
设AC与BD的交点为O,连接B1O,则AC⊥OB1.
∵B1A=B1C=
22+(
|
| 6 |
| 2 |
(
|
∴S△AB1C=
| 1 |
| 2 |
| 2 |
| 2 |
而S△B1C1C=
| 1 |
| 2 |
| 2 |
| 2 |
∴h=
| S△B1C1C•AB |
| S△AB1C |
| ||
2
|
点评:熟练掌握正方形的性质、线面垂直的判定和性质定理、“等积变形”、等腰三角形的性质是解题的关键.

练习册系列答案
相关题目
 如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为:
如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为: 如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )
如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )

 .
. 
 ,AA1 =
,AA1 = ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.