题目内容
已知函数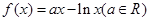 。
。
(1)当 时,求曲线
时,求曲线 在
在 处切线的斜率;
处切线的斜率;
(2)求 的单调区间;
的单调区间;
(3)当 时,求
时,求 在区间
在区间 上的最小值。
上的最小值。
(1)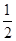 ;(2)当
;(2)当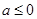 时,
时, 的单调递减区间为
的单调递减区间为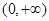 ;当
;当 时,函数
时,函数 的单调递减区间为
的单调递减区间为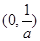 ,单调递增区间为
,单调递增区间为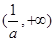 。(3)
。(3)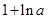 ;
;
解析试题分析:(1)把 代入函数解析式中,求出函数的导数,把
代入函数解析式中,求出函数的导数,把 代入导函数中去即得切线的斜率
代入导函数中去即得切线的斜率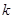 ;(2)求出导函数,导函数中含有参数
;(2)求出导函数,导函数中含有参数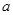 ,要对
,要对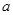 进行讨论,然后令导函数大于0得增区间,令导函数小于0得减区间;(3)利用(2)中求得的单调区间来求函数的最值即可,但要对
进行讨论,然后令导函数大于0得增区间,令导函数小于0得减区间;(3)利用(2)中求得的单调区间来求函数的最值即可,但要对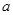 在范围
在范围 内进行讨论;
内进行讨论;
试题解析:解:(1)当 时,
时,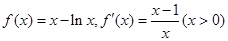 , 2分
, 2分
故曲线 在
在 处切线的斜率为
处切线的斜率为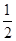 。 4分
。 4分
(2)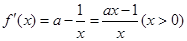 。 6分
。 6分
①当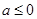 时,由于
时,由于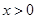 ,故
,故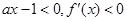 。
。
所以, 的单调递减区间为
的单调递减区间为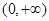 。 8分
。 8分
②当 时,由
时,由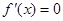 ,得
,得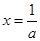 。
。
在区间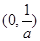 上,
上,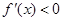 ,在区间
,在区间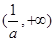 上,
上,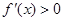 。
。
所以,函数 的单调递减区间为
的单调递减区间为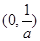 ,单调递增区间为
,单调递增区间为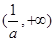 。 10分
。 10分
综上,当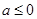 时,
时, 的单调递减区间为
的单调递减区间为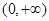 ;当
;当 时,函数
时,函数 的单调递减区间为
的单调递减区间为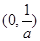 ,单调递增区间为
,单调递增区间为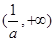 。 11分
。 11分
(3)根据(2)得到的结论,当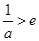 ,即
,即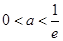 时,
时, 在区间
在区间 上的最小值为
上的最小值为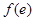 ,
,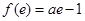 。 13分
。 13分
当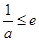 ,即
,即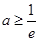 时,
时, 在区间
在区间 上的最小值为
上的最小值为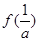 ,
,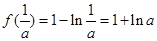 。
。
综上,当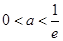 时,
时, 在区间
在区间 上的最小值为
上的最小值为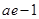 ,当
,当

练习册系列答案
相关题目
 ,
, ,
, .
. 时,求函数
时,求函数 的最小值;
的最小值; ,令
,令 ,求
,求 的取值范围.
的取值范围.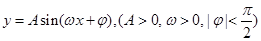 的最小值是
的最小值是 ,在一个周期内图象最高点与最低点横坐标差是
,在一个周期内图象最高点与最低点横坐标差是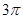 ,又:图象过点
,又:图象过点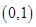 ,
, 的集合;
的集合; .
. 的定义域;
的定义域;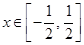 时,函数
时,函数 ,求函数
,求函数 的值域.
的值域. 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若
,若 时,有
时,有

 对
对 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围 上的奇函数
上的奇函数 ,当
,当 时,
时,
 上单调递增,求实数
上单调递增,求实数 的取值范围。
的取值范围。 +1,h(x)=
+1,h(x)= ,x∈(-3,a],其中a为常数且a>0,令函数f(x)=g(x)·h(x).
,x∈(-3,a],其中a为常数且a>0,令函数f(x)=g(x)·h(x). 时,求函数f(x)的值域.
时,求函数f(x)的值域. 上单调递减,则
上单调递减,则 的取值范围为 .
的取值范围为 .