题目内容
已知函数 在其定义域上为奇函数.
在其定义域上为奇函数.
⑴求m的值;
⑵若关于x的不等式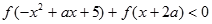 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)m=7;(2) .
.
解析试题分析:
(1)由 是奇函数得:
是奇函数得: 所以
所以 即
即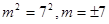 ;然后对m=-7和m=7检验即可;
;然后对m=-7和m=7检验即可;
(2)先由(1)及复合函数的单调性确定函数 的单调性,再利用函数的奇偶性和单调性将已知不等式转化为一般的代数不等式,最后用分离参数法,将不等式的恒成立问题转化为函数的最值问题进行解决.
的单调性,再利用函数的奇偶性和单调性将已知不等式转化为一般的代数不等式,最后用分离参数法,将不等式的恒成立问题转化为函数的最值问题进行解决.
试题解析:(1)由 是奇函数得:
是奇函数得: 所以
所以 即
即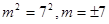 ;
;
当m=-7时, ,舍去;
,舍去;
当 时,
时,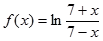 ,由
,由 得定义域为
得定义域为 .
.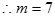 .
.
⑵设 在
在 是增函数,
是增函数,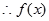 在
在 是增函数.又
是增函数.又
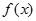 为奇函数,
为奇函数,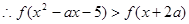 ,
, 对任意实数
对任意实数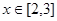 恒成立;
恒成立;
对于 ,即
,即 .
.
令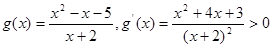 恒成立,
恒成立,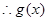 在[2,3]上递增,
在[2,3]上递增, ,则
,则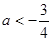 ;
;
对于 ,
, 在[2,3]上递增,
在[2,3]上递增, ,则
,则 ;
;
对于 ,即
,即
 ,则
,则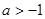 ;
;
综上, 的取值范围是
的取值范围是 .
.
考点:1.函数的奇偶性;2.利用函数的单调性解不等式;3.不等式的恒成立.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
 ,
, ,
, .
. 时,求函数
时,求函数 的最小值;
的最小值; ,令
,令 ,求
,求 的取值范围.
的取值范围. .
. 的定义域;
的定义域;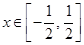 时,函数
时,函数 ,求函数
,求函数 的值域.
的值域. 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若
,若 时,有
时,有

 对
对 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围 上函数
上函数 为奇函数.
为奇函数. 的值;
的值; 的值域.
的值域. 上的奇函数
上的奇函数 ,当
,当 时,
时,
 上单调递增,求实数
上单调递增,求实数 的取值范围。
的取值范围。 为偶函数,曲线
为偶函数,曲线 过点
过点 ,
,  .
. 有斜率为0的切线,求实数
有斜率为0的切线,求实数 的取值范围;
的取值范围; 时函数
时函数 的定义域.
的定义域. 的反函数的图像过点
的反函数的图像过点 ,则
,则