题目内容
5.若$m=\sqrt{3}+\sqrt{5}$,$n=\sqrt{2}+\sqrt{6}$,则下列结论正确的是( )| A. | m<n | B. | n<m | ||
| C. | n=m | D. | 不能确定m,n的大小 |
分析 分别求出m2=8+2$\sqrt{15}$,n2=8+2$\sqrt{12}$,易知m2>n2,即可得到m>n.
解答 解:∵$m=\sqrt{3}+\sqrt{5}$,$n=\sqrt{2}+\sqrt{6}$,
∴m2=8+2$\sqrt{15}$,n2=8+2$\sqrt{12}$,
∴m2>n2,
∴m>n,
故选:B.
点评 本题考查了不等式的大小比较的方法,采用平方法,属于基础题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
20.已知圆O:x2+y2=1,点M(x0,y0)是直线上x-y+2=0一点,若圆O上存在一点N,使得∠NMO=$\frac{π}{6}$,则x0的取值范围是( )
| A. | [-2,0] | B. | (0,3) | C. | [2,4] | D. | (-1,3) |
14.不论m如何变化,直线(m+2)x-(2m-1)y-(3m-4)=0恒过定点( )
| A. | (1,2) | B. | (-1,-2) | C. | (2,1) | D. | (-2,-1) |
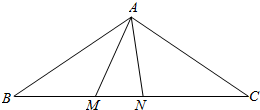 如图,在等腰△ABC中,∠BAC=120°,AB=$\sqrt{3}$,点M在线段BC上.
如图,在等腰△ABC中,∠BAC=120°,AB=$\sqrt{3}$,点M在线段BC上.