题目内容
10.如图,正方体ABCD-A1B1C1D1的棱长为1,P对角线BD1的三等分点,P到直线CC1的距离为$\frac{\sqrt{5}}{3}$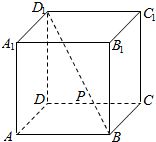
分析 如图所示,连接B1D1,作MP∥B1B,连接C1M,则C1M等于P到直线CC1的距离,利用余弦定理,求出C1M即可.
解答  解:如图所示,连接B1D1,作MP∥B1B,连接C1M,则C1M等于P到直线CC1的距离.
解:如图所示,连接B1D1,作MP∥B1B,连接C1M,则C1M等于P到直线CC1的距离.
∵P对角线BD1的三等分点,
∴B1M=$\frac{\sqrt{2}}{3}$,
∴C1M=$\sqrt{1+\frac{2}{9}-2×1×\frac{\sqrt{2}}{3}×\frac{\sqrt{2}}{2}}$=$\frac{\sqrt{5}}{3}$,
∴P到直线CC1的距离等于$\frac{\sqrt{5}}{3}$.
故答案为:$\frac{\sqrt{5}}{3}$.
点评 本题考查求P到直线CC1的距离,考查余弦定理的运用,正确转化是关键.

练习册系列答案
相关题目
15.若2cos($\frac{π}{2}$-α)-sin($\frac{3}{2}$π+α)=-$\sqrt{5}$,则tanα=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
5.若$m=\sqrt{3}+\sqrt{5}$,$n=\sqrt{2}+\sqrt{6}$,则下列结论正确的是( )
| A. | m<n | B. | n<m | ||
| C. | n=m | D. | 不能确定m,n的大小 |
 已知在四棱锥S-ABCD中,四边形ABCD是菱形,SD⊥平面ABCD,P为SB的中点,Q为BD上一动点.AD=2,SD=2,∠DAB=$\frac{π}{3}$.
已知在四棱锥S-ABCD中,四边形ABCD是菱形,SD⊥平面ABCD,P为SB的中点,Q为BD上一动点.AD=2,SD=2,∠DAB=$\frac{π}{3}$.