题目内容
10.(文)若正数x,y满足x+y+xy=8,则xy的最大值为4.分析 由题意和基本不等式可得$\sqrt{xy}$的不等式,解不等式可得.
解答 解:∵正数x,y满足x+y+xy=8,
∴8-xy=x+y≥2$\sqrt{xy}$,
∴($\sqrt{xy}$)2+2$\sqrt{xy}$-8≤0,
解得-4≤$\sqrt{xy}$≤2,
故xy≤4,当且仅当x=y=2时取等号.
∴xy的最大值为4
故答案为:4
点评 本题考查基本不等式,涉及不等式的解法和整体思想,属基础题.

练习册系列答案
相关题目
15.若2cos($\frac{π}{2}$-α)-sin($\frac{3}{2}$π+α)=-$\sqrt{5}$,则tanα=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
1.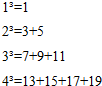 已知任意一个正整数的三次幂均可表示成一些连续奇数的和,如图所示,33可以表示为7+9+11,我们把7,9,11叫做33的“质数因子”,若n3的一个“质数因子”为2013,则n为( )
已知任意一个正整数的三次幂均可表示成一些连续奇数的和,如图所示,33可以表示为7+9+11,我们把7,9,11叫做33的“质数因子”,若n3的一个“质数因子”为2013,则n为( )
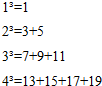 已知任意一个正整数的三次幂均可表示成一些连续奇数的和,如图所示,33可以表示为7+9+11,我们把7,9,11叫做33的“质数因子”,若n3的一个“质数因子”为2013,则n为( )
已知任意一个正整数的三次幂均可表示成一些连续奇数的和,如图所示,33可以表示为7+9+11,我们把7,9,11叫做33的“质数因子”,若n3的一个“质数因子”为2013,则n为( )| A. | 43 | B. | 44 | C. | 45 | D. | 46 |
5.若$m=\sqrt{3}+\sqrt{5}$,$n=\sqrt{2}+\sqrt{6}$,则下列结论正确的是( )
| A. | m<n | B. | n<m | ||
| C. | n=m | D. | 不能确定m,n的大小 |
19.已知三点A(2,2),B(3,1),C(-1,-1),则过点A的直线l与线段BC有公共点时(公共点包含公共点),直线l的斜率kl的取值范围是( )
| A. | [-1,1] | B. | (-∞,-1]∪[1,+∞) | C. | (-1,1) | D. | (-∞,-1)∪(1,+∞) |
20.函数f(x)=$\sqrt{2-x}$+$\sqrt{x}$的定义域为( )
| A. | (2,+∞) | B. | (-∞,0) | C. | (0,2) | D. | [0,2] |