题目内容
设点P是双曲线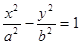 上除顶点外的任意一点,F1,F2分别为左、右焦点,c 为半焦距,
上除顶点外的任意一点,F1,F2分别为左、右焦点,c 为半焦距,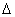 PF1F2的内切圆与边F1F2切于点M,求|F1M|·|F2M|=
PF1F2的内切圆与边F1F2切于点M,求|F1M|·|F2M|=
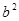
解析试题分析:解:根据从圆外一点向圆所引的两条切线长相等可知: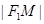 =
=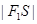 ,
,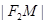 =
=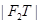 |,|PS|=|PT|
|,|PS|=|PT|
①当P在双曲线图象的右支时,而根据双曲线的定义可知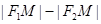 =
=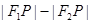 =2a①;
=2a①;
而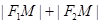 =
=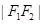 =2c②,
=2c②,
联立①②解得: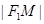 =a+c,
=a+c,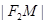 =c-a,所
=c-a,所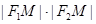 =(a+c)(c-a)=c2-a2=b2;
=(a+c)(c-a)=c2-a2=b2;
②当P在双曲线图象的左支时,而根据双曲线的定义可知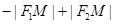 =
=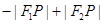 =2a③;
=2a③;
而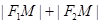 =
=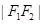 =2c④,
=2c④,
联立③④解得: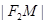 =a+c,
=a+c,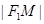 =c-a,
=c-a,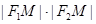 =(a+c)(c-a)=c2-a2=b2.
=(a+c)(c-a)=c2-a2=b2.
综上,可得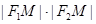 =b2.
=b2.
故答案为:b2
考点:双曲线的性质
点评:考查学生掌握双曲线的基本性质,灵活运用圆切线长定理化简求值.做题时注意利用分类讨论的数学思想

练习册系列答案
相关题目
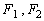 为双曲线
为双曲线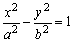 的左右焦点,点P在双曲线上,
的左右焦点,点P在双曲线上,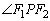 的平分线分线段
的平分线分线段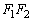 的比为5∶1,则双曲线的离心率的取值范围是 .
的比为5∶1,则双曲线的离心率的取值范围是 .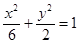 和双曲线
和双曲线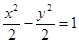 的公共焦点为
的公共焦点为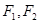 ,
,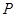 是两曲线的一个交点,则
是两曲线的一个交点,则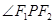 = .
= .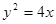 上一点
上一点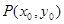 到其焦点
到其焦点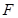 的距离等于4,则
的距离等于4,则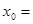
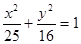 的左右焦点为
的左右焦点为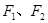 ,弦
,弦 过点
过点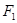 ,若△
,若△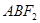 的内切圆周长为
的内切圆周长为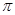 ,点
,点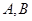 坐标分别为
坐标分别为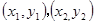 ,则
,则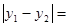 。
。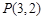 且与双曲线
且与双曲线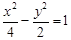 有相同渐近线方程的双曲线的标准方程为 .
有相同渐近线方程的双曲线的标准方程为 . 的方程
的方程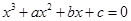 的三个根可分别作为一个椭圆、双曲线、抛物线的离心率,则
的三个根可分别作为一个椭圆、双曲线、抛物线的离心率,则 的取值范围为 .
的取值范围为 . 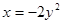 的准线方程是
的准线方程是  长轴的一个顶点作圆
长轴的一个顶点作圆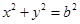 的两条切线,切点分别为
的两条切线,切点分别为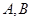 ,若
,若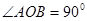 (
(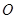 是坐标原点),则椭圆
是坐标原点),则椭圆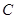 的离心率为_________.
的离心率为_________.