题目内容
椭圆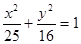 的左右焦点为
的左右焦点为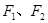 ,弦
,弦 过点
过点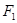 ,若△
,若△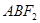 的内切圆周长为
的内切圆周长为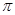 ,点
,点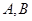 坐标分别为
坐标分别为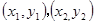 ,则
,则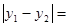 。
。

解析试题分析:先根据椭圆方程求得a和c,及左右焦点的坐标,进而根据三角形内切圆面积求得内切圆半径,进而根据△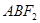 的面积=△
的面积=△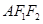 的面积+△
的面积+△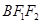 的面积求得△ABF2的面积=3|y2-y1|进而根据内切圆半径和三角形周长求得其面积,建立等式求得|y2-y1|的值.
的面积求得△ABF2的面积=3|y2-y1|进而根据内切圆半径和三角形周长求得其面积,建立等式求得|y2-y1|的值.
根据椭圆方程,可知a=5,b=4,∴c=3,
左、右焦点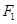 (-3,0)、
(-3,0)、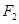 ( 3,0),△
( 3,0),△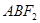 的内切圆面积为π,则内切圆的半径为r=
的内切圆面积为π,则内切圆的半径为r=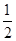 ,而
,而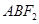 的面积=△
的面积=△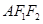 的面积+△
的面积+△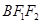 的面积==3
的面积==3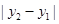 ,
,
又△ABF2的面积═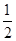 ×r(
×r(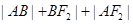 =
=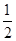 ×
×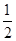 (2a+2a)=a=5,3
(2a+2a)=a=5,3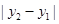 =5,
=5,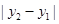 =
= ,故答案为
,故答案为
考点:椭圆的方程
点评:本题主要考查了直线与圆锥曲线的综合问题,椭圆的简单性质,三角形内切圆性质,本题的关键是求出△ABF2的面积,属于中档题

练习册系列答案
相关题目
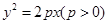 的焦点F的直线
的焦点F的直线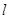 依次交抛物线及其准线于点A、B、C,若|BC |=2|BF|,且|AF|=3,则抛物线的方程是 。
依次交抛物线及其准线于点A、B、C,若|BC |=2|BF|,且|AF|=3,则抛物线的方程是 。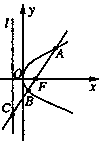
 的一条渐近线方程为
的一条渐近线方程为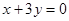 ,则此双曲线的离心率为 。
,则此双曲线的离心率为 。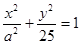 (
(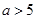 ),它的两个焦点分别为
),它的两个焦点分别为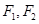 ,且
,且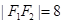 ,弦AB(椭圆上任意两点的线段)过点
,弦AB(椭圆上任意两点的线段)过点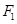 ,则
,则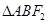 的周长为
的周长为 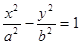 上除顶点外的任意一点,F1,F2分别为左、右焦点,c 为半焦距,
上除顶点外的任意一点,F1,F2分别为左、右焦点,c 为半焦距, PF1F2的内切圆与边F1F2切于点M,求|F1M|·|F2M|=
PF1F2的内切圆与边F1F2切于点M,求|F1M|·|F2M|= 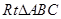 中,
中,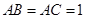 ,以点
,以点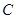 为一个焦点作一个椭圆,使这个椭圆的另一焦点在
为一个焦点作一个椭圆,使这个椭圆的另一焦点在 边上,且这个椭圆过
边上,且这个椭圆过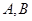 两点,则这个椭圆的焦距长为 .
两点,则这个椭圆的焦距长为 . 的焦点为
的焦点为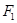 、
、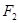 ,点
,点 在双曲线上且
在双曲线上且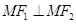 ,则点
,则点 轴的距离为 .
轴的距离为 .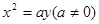 的准线方程是 ____________.
的准线方程是 ____________.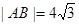 ,则双曲线C的方程为__________.
,则双曲线C的方程为__________.