题目内容
9.已知函数$f(x)=\frac{ax+b}{{1+{x^2}}}$为奇函数,且定义域为(-1,1),$f(\frac{1}{2})=\frac{2}{5}$,求f(x)的解析式.分析 由函数f(x)是定义在(-1,1)上的奇函数,所以f(0)=0,再据$f(\frac{1}{2})=\frac{2}{5}$可求出a的值,即可求f(x)的解析式.
解答 解:∵函数$f(x)=\frac{ax+b}{{1+{x^2}}}$是定义域为(-1,1)上的奇函数,
∴f(0)=0,∴b=0;
又$f(\frac{1}{2})=\frac{2}{5}$,∴$\frac{\frac{1}{2}a}{1+\frac{1}{4}}$=$\frac{2}{5}$
∴a=1.
∴f(x)=$\frac{x}{1+{x}^{2}}$.
点评 本题考查了函数的奇偶性,充分理解以上性质是解决问题的关键.利用已证结论解决问题是常用的方法,注意体会和使用.

练习册系列答案
相关题目
20.已知函数f(x)=$\left\{\begin{array}{l}{1-{e}^{-x},x≤0}\\{\sqrt{2x},x>0}\end{array}\right.$,若|f(x)|≥ax,则实数a的取值范围为( )
| A. | (-∞,0] | B. | (-∞,-1] | C. | [-2,0] | D. | [-1,0] |
17.己知集合M={x|-2<x<3},N={x|lgx≥0},则M∩N=( )
| A. | (-2,+∞) | B. | [1,3) | C. | (-2,-1] | D. | (-2,3) |
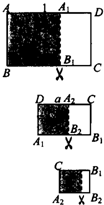 长为1,宽为a($\frac{1}{2}$<a<1)的矩形纸片,剪下一个边长等于矩形宽度的正方形(称为第1次操作),剩下矩形长为原矩形的宽,如图,再剪下一个边长等于此时矩形宽度的正方形(称为第2次操作),剩下矩形长为第二个矩形的宽,如此反复操作下去,若在第n次操作后,剩下的矩形为正方形,则操作终止.
长为1,宽为a($\frac{1}{2}$<a<1)的矩形纸片,剪下一个边长等于矩形宽度的正方形(称为第1次操作),剩下矩形长为原矩形的宽,如图,再剪下一个边长等于此时矩形宽度的正方形(称为第2次操作),剩下矩形长为第二个矩形的宽,如此反复操作下去,若在第n次操作后,剩下的矩形为正方形,则操作终止.