题目内容
6.已知函数f(x)=x2+ax+b(a、b∈R)的两个零点为x1、x2,并且0<x1<1<x2<2,则a2+b2-6b的取值范围是( )| A. | [-1,4) | B. | (-1,4) | C. | (1,4) | D. | [-4,1) |
分析 根据题意,由函数根的分布情况可得$\left\{\begin{array}{l}{f(0)>0}\\{f(1)<0}\\{f(2)>0}\end{array}\right.$,进而可以利用平面区域表示出来,而a2+b2-6b=a2+(b-3)2-9,可以设t=$\sqrt{{a}^{2}+(b-3)^{2}}$,分析易得t的几何意义,借助线性规划的内容分析易得t的取值范围,由a2+b2-6b=t2-9分析可得答案.
解答 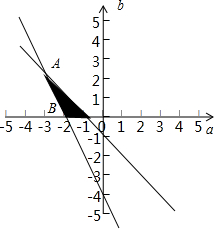 解:根据题意,若函数f(x)=x2+ax+b(a、b∈R)的两个零点为x1、x2,并且0<x1<1<x2<2,
解:根据题意,若函数f(x)=x2+ax+b(a、b∈R)的两个零点为x1、x2,并且0<x1<1<x2<2,
则有$\left\{\begin{array}{l}{f(0)>0}\\{f(1)<0}\\{f(2)>0}\end{array}\right.$,即$\left\{\begin{array}{l}{b>0}\\{a+b+1<0}\\{4+2a+b>0}\end{array}\right.$,
可以用如图的阴影部分表示:(不含边界)
而a2+b2-6b=a2+(b-3)2-9,
令t2=a2+(b-3)2,则t=$\sqrt{{a}^{2}+(b-3)^{2}}$,
则t的几何意义为阴影区域内的点与点(0,3)之间的距离,
分析易得:t的取值范围是(2$\sqrt{2}$,$\sqrt{13}$),
则a2+b2-6b=t2-9的范围为(-1,4);
故选:B.
点评 本题考查线性规划的运用,解题的关键是将一元二次方程根的分布情况转化为不等式组,进而用线性规划进行分析.

练习册系列答案
相关题目
6.下列说法正确的是( )
| A. | log0.56>log0.54 | B. | 0.60.5>log0.60.5 | ||
| C. | 2.50<${(\frac{1}{2})^{2.5}}$ | D. | 90.9>270.48 |
18.观察下列各式:a1+b1+c1=2,a2+b2+c2=3,a3+b3+c3=5,a4+b4+c4=8,a5+b5+c5=13…,则a10+b10+c10=( )
| A. | 89 | B. | 144 | C. | 233 | D. | 232 |
15.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+\frac{1}{2}x(x<0)}\\{ln(x+1)(x≥0)}\end{array}\right.$,若函数y=f(x)-kx有3个零点,则实数k的取值范围为( )
| A. | $(0,\frac{1}{2})$ | B. | $(\frac{1}{2},1)$ | C. | (1,+∞) | D. | $(\frac{1}{4},1)$ |