题目内容
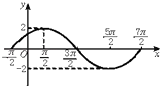
【题目】已知函数f（x）=Asin（x+φ）（A＞0，0＜φ＜π），x∈R的最大值是1，其图象经过点 
．
（1）求f（x）的解析式；
（2）已知 
，且 
， 
，求f（α﹣β）的值．
【答案】
（1）解：依题意有A=1，则f（x）=sin（x+φ），将点 
代入得 
，而0＜φ＜π，∴ 
，∴ 
，故 
（2）解：依题意有 
，而 
，∴ 
， 
【解析】（1）根据题意求出A，图象经过点 ，代入方程求出φ，然后求f（x）的解析式；（2） ，且 
， 
，求出 ，然后求出sinα，sinβ，利用两角差的余弦函数求f（α﹣β）的值．
【考点精析】通过灵活运用两角和与差的余弦公式，掌握两角和与差的余弦公式：
即可以解答此题．
练习册系列答案
相关题目
【题目】下表提供了某厂节能降耗技术改造后生产产品过程中记录的产量x（吨）与相应的生产能耗y（吨）标准煤的几组对照数据：
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
（1）求y关于x的线性回归方程；（已知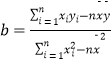 
）
（2）已知该厂技术改造前100吨甲产品能耗为90吨标准煤，试根据（1）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技术改造前降低了多少吨标准煤．
【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷，按事先拟定的价格进行5天试销，每种单价试销1天，得到如表数据：
单价x（元） | 18 | 19 | 20 | 21 | 22 |
销量y（册） | 61 | 56 | 50 | 48 | 45 |
（1）求试销5天的销量的方差和y对x的回归直线方程；
（2）预计今后的销售中，销量与单价服从（1）中的回归方程，已知每册单元卷的成本是14元，
为了获得最大利润，该单元卷的单价应定为多少元？
