题目内容
14.如图EF为两条直线l1、l2的公垂线段,且EF=9,点B、D分别在两平行直线上运动,且A、B、C、D满足$\overrightarrow{FA}$=2$\overrightarrow{AE}$,$\overrightarrow{AB}$+$\overrightarrow{CD}$=0,$\overrightarrow{AC}$•$\overrightarrow{BD}$=0.(1)如图1,若点B,D在线段EF同侧运动,且∠BAD=60°,试求四边形ABCD的面积;
(2)如图2,若点B,D在线段EF异侧侧运动,试求四边形ABCD的面积的最小值;
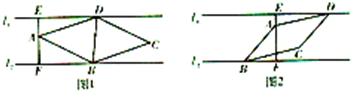
分析 (1)根据$\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{0}$,$\overrightarrow{AC}$•$\overrightarrow{BD}$=0得出四边形ABCD是菱形;在Rt△FAD与Rt△ABF中,由∠BAD=60°,利用三角恒等变换求出边长AD的值,再计算菱形ABCD的面积;
(2)设∠ABC=α,∠CBF=β,在Rt△AED与Rt△ABF中,得出α与β的关系,写出菱形ABCD面积表达式,再利用三角函数的图象与性质求出它的最小值即可.
解答 解:(1)∵$\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{0}$,$\overrightarrow{AC}$•$\overrightarrow{BD}$=0,∴四边形ABCD是菱形;
又∵$\overrightarrow{FA}$=2$\overrightarrow{AE}$,EF=9,∴AE=3,AF=6;
设AD=x,在Rt△FAD与Rt△ABF中,
cos∠EAD=$\frac{3}{x}$,cos∠FAB=$\frac{6}{x}$,
sin∠EAD=$\frac{\sqrt{{x}^{2}-9}}{x}$,sin∠FAB=$\frac{\sqrt{{x}^{2}-36}}{x}$;
又∠BAD=60°,∴∠EAD+∠FAB=120°,
∴cos(∠EAD+∠FAB)=-$\frac{1}{2}$,
即$\frac{3}{x}$•$\frac{6}{x}$-$\frac{\sqrt{{x}^{2}-9}}{x}$•$\frac{\sqrt{{x}^{2}-36}}{x}$=-$\frac{1}{2}$,
解得x=2$\sqrt{21}$;
∴菱形ABCD的面积为S=x2•sin60°=42$\sqrt{3}$;
(2)设∠ABC=α,∠CBF=β,其中α∈(0,$\frac{π}{3}$),β∈(0,$\frac{π}{6}$);
再设AB=x,则在Rt△AED与Rt△ABF中,有$\left\{\begin{array}{l}{xsinβ=3}\\{xsin(α+β)=6}\end{array}\right.$;
两式相除得sin(α+β)=2sinβ,
由此可得tanβ=$\frac{sinα}{2-cosα}$,
∴菱形ABCD的面积为
S′=x2sinα=$\frac{9}{{sin}^{2}β}$•sinα=9sinα•(1+$\frac{1}{{tan}^{2}β}$)=9•$\frac{5-4cosα}{sinα}$;
令t=$\frac{5-4cosα}{sinα}$,则tsinα+4cosα=5,
∴$\sqrt{{t}^{2}+16}$sin(α+φ)=5,
∴sin(α+φ)=$\frac{5}{\sqrt{{t}^{2}+16}}$≤1,
解得t≥3;
∴当t=3时,3sinα+4cosα=5,
此时sinα=$\frac{3}{5}$,cosα=$\frac{4}{5}$符合题意;
∴菱形ABCD面积的最小值为27.
点评 本题考查了平面向量的应用问题,也考查了三角函数的图象与性质的应用问题,是综合性题目.

 一线名师权威作业本系列答案
一线名师权威作业本系列答案