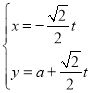题目内容
【题目】已知
，
，
，
是半径为2的球面上的点，
，
，点在
上的射影为
，则三棱锥
体积的最大值是（ ）.
A.
B.
C.
D.
【答案】B
【解析】
由
可以判断出点
在底面的射影的位置，这样可以确定球心位置，利用勾股定理、直角三角形的性质可以求出点到底面
的距离，利用相似三角形的性质，可以求出三角形的面积表达式，最后利用导数求出其面积的最大值，最后也就求出了体积的最大值,
因为，
，所以点在底面的射影
是直角三角形
斜边
中点，所以球心
在线段
的延长线上，设
，因此
，
，即
，
.
过
作
，垂足为
，设
，
，
，
由
，可得
，
，
设
，则有
，由
，可得
，
当
时，
，函数单调递增，
当
时，
，函数单调递减，故当，函数有最大值，最大值为：
.三角形的面积的最大值为
.
三棱锥
体积的最大值是
.
故选：B
【题目】某品牌汽车4S店，对该品牌旗下的A型、B型、C型汽车进行维修保养，汽车4S店记录了100辆该品牌三种类型汽车的维修情况，整理得下表：
车型 | A型 | B型 | C型 |
频数 | 20 | 40 | 40 |
假设该店采用分层抽样的方法从上述维修的100辆该品牌三种类型汽车中随机取10辆进行问卷回访．
（1）求A型、B型、C型各车型汽车抽取的数目；
（2）维修结束后这100辆汽车的司机采用“100分制”打分的方式表示对4S店的满意度，按照大于等于80为优秀，小于80为合格，得到如下列联表：
优秀 | 合格 | 合计 | |
男司机 | 10 | 38 | 48 |
女司机 | 25 | 27 | 52 |
合计 | 35 | 65 | 100 |
问能否在犯错误概率不超过0.01的前提下认为司机对4S店满意度与性别有关系？请说明原因．
（参考公式：
）
附表：
| 0.100 | 0.050 | 0.010 | 0.001 |
K | 2.706 | 3.841 | 6.635 | 10.828 |
【题目】某汽车美容公司为吸引顾客，推出优惠活动：对首次消费的顾客，按200元/次收费，并注册成为会员，对会员逐次消费给予相应优惠，标准如下：
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | ≥5次 |
收费比率 | 1 | 0.95 | 0.90 | 0.85 | 0.80 |
该公司注册的会员中没有消费超过5次的，从注册的会员中，随机抽取了100位进行统计，得到统计数据
如下：
消费次数 | 1次 | 2次 | 3次 | 4次 | 5次 |
人数 | 60 | 20 | 10 | 5 | 5 |
假设汽车美容一次，公司成本为150元，根据所给数据，解答下列问题：
（1）某会员仅消费两次，求这两次消费中，公司获得的平均利润；
（2）以事件发生的频率作为相应事件发生的概率， 设该公司为一位会员服务的平均利润为
元，求大于40的概率.
