题目内容
在非负数构成的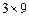 数表
数表
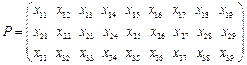
中每行的数互不相同,前6列中每列的三数之和为1,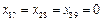 ,
,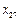 ,
,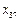 ,
,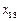 ,
,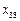 ,
,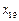 ,
,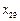 均大于.如果
均大于.如果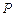 的前三列构成的数表
的前三列构成的数表
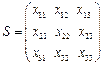
满足下面的性质 :对于数表
:对于数表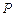 中的任意一列
中的任意一列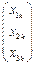 (
(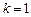 ,2,…,9)均存在某个
,2,…,9)均存在某个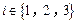
使得
⑶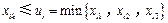 .
.
求证:
(ⅰ)最小值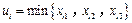 ,
, ,2,3一定自数表
,2,3一定自数表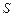 的不同列.
的不同列.
(ⅱ)存在数表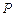 中唯一的一列
中唯一的一列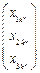 ,
,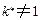 ,2,3使得
,2,3使得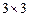 数表
数表
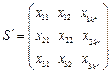
仍然具有性质 .
.
 数表
数表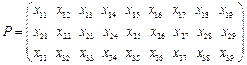
中每行的数互不相同,前6列中每列的三数之和为1,
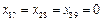 ,
,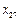 ,
,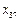 ,
,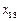 ,
,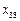 ,
,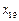 ,
,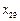 均大于.如果
均大于.如果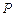 的前三列构成的数表
的前三列构成的数表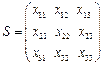
满足下面的性质
 :对于数表
:对于数表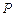 中的任意一列
中的任意一列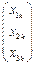 (
(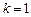 ,2,…,9)均存在某个
,2,…,9)均存在某个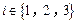
使得
⑶
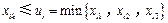 .
.求证:
(ⅰ)最小值
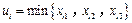 ,
, ,2,3一定自数表
,2,3一定自数表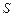 的不同列.
的不同列.(ⅱ)存在数表
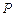 中唯一的一列
中唯一的一列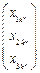 ,
,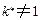 ,2,3使得
,2,3使得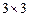 数表
数表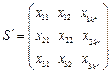
仍然具有性质
 .
.(ⅰ)假设最小值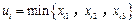 ,
, ,2,3不是取自数表
,2,3不是取自数表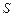 的不同列.则存在一列不含任何
的不同列.则存在一列不含任何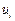 .不妨设
.不妨设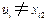 ,
, ,2,3.由于数表
,2,3.由于数表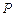 中同一行中的任何两个元素都不等,于是
中同一行中的任何两个元素都不等,于是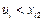 ,
, ,2,3.另一方面,由于数表
,2,3.另一方面,由于数表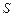 具有性质
具有性质 ,在⑶中取
,在⑶中取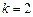 ,则存在某个
,则存在某个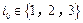 使得
使得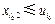 .矛盾.
.矛盾.
(ⅱ)由抽届原理知
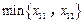 ,
,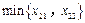 ,
,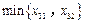
中至少有两个值取在同一列.不妨设
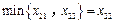 ,
,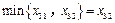 .
.
由前面的结论知数表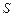 的第一列一定含有某个
的第一列一定含有某个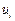 ,所以只能是
,所以只能是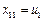 .同样,第二列中也必含某个
.同样,第二列中也必含某个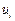 ,
, ,2.不妨设
,2.不妨设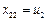 .于是
.于是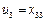 ,即
,即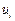 是数表
是数表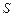 中的对角线上数字.
中的对角线上数字.
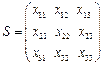
记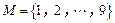 ,令集合
,令集合
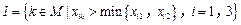 .
.
显然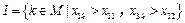 且1,2
且1,2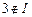 .因为
.因为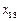 ,
,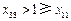 ,
,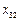 ,所以
,所以 .
.
故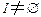 .于是存在
.于是存在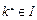 使得
使得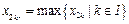 .显然,
.显然,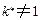 ,2,3.
,2,3.
下面证明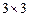 数表
数表
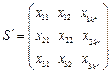
具有性质 .
.
从上面的选法可知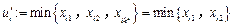 ,
,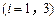 .这说明
.这说明
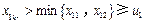 ,
,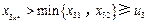 .
.
又由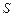 满足性质
满足性质 .在⑶中取
.在⑶中取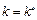 ,推得
,推得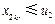 ,于是
,于是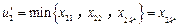 .下证对任意的
.下证对任意的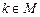 ,存在某个
,存在某个 ,2,3使得
,2,3使得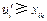 .假若不然,则
.假若不然,则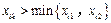 ,
, ,3且
,3且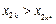 .这与
.这与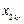 的最大性矛盾.因此,数表
的最大性矛盾.因此,数表 满足性质
满足性质 .
.
下证唯一性.设有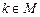 使得数表
使得数表
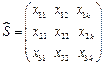
具有性质 ,不失一般性,我们假定
,不失一般性,我们假定
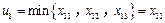
⑷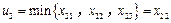
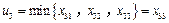
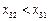 .
.
由于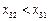 ,
,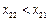 及(ⅰ),有
及(ⅰ),有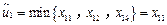 .又由(ⅰ)知:或者
.又由(ⅰ)知:或者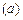
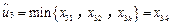 ,或者
,或者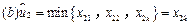 .
.
如果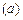 成立,由数表
成立,由数表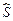 具有性质
具有性质 ,则
,则
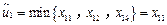 ,
,
⑸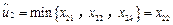 ,
,
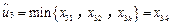 .
.
由数表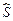 满足性质
满足性质 ,则对于
,则对于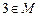 至少存在一个
至少存在一个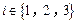 使得
使得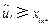 .由
.由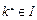 及⑷和⑹式知,
及⑷和⑹式知,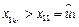 ,
,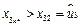 .于是只能有
.于是只能有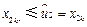 .类似地,由
.类似地,由 满足性质
满足性质 及
及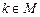 可推得
可推得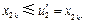 .从而
.从而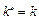 .
.
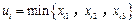 ,
, ,2,3不是取自数表
,2,3不是取自数表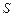 的不同列.则存在一列不含任何
的不同列.则存在一列不含任何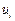 .不妨设
.不妨设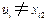 ,
, ,2,3.由于数表
,2,3.由于数表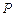 中同一行中的任何两个元素都不等,于是
中同一行中的任何两个元素都不等,于是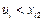 ,
, ,2,3.另一方面,由于数表
,2,3.另一方面,由于数表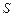 具有性质
具有性质 ,在⑶中取
,在⑶中取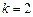 ,则存在某个
,则存在某个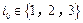 使得
使得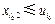 .矛盾.
.矛盾.(ⅱ)由抽届原理知
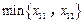 ,
,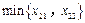 ,
,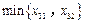
中至少有两个值取在同一列.不妨设
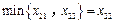 ,
,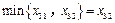 .
.由前面的结论知数表
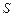 的第一列一定含有某个
的第一列一定含有某个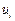 ,所以只能是
,所以只能是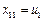 .同样,第二列中也必含某个
.同样,第二列中也必含某个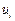 ,
, ,2.不妨设
,2.不妨设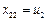 .于是
.于是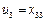 ,即
,即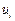 是数表
是数表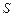 中的对角线上数字.
中的对角线上数字.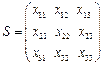
记
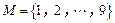 ,令集合
,令集合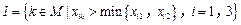 .
.显然
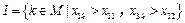 且1,2
且1,2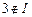 .因为
.因为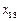 ,
,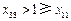 ,
,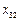 ,所以
,所以 .
.故
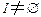 .于是存在
.于是存在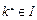 使得
使得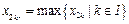 .显然,
.显然,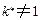 ,2,3.
,2,3.下面证明
 数表
数表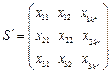
具有性质
 .
.从上面的选法可知
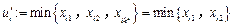 ,
,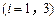 .这说明
.这说明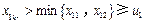 ,
,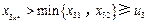 .
.又由
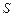 满足性质
满足性质 .在⑶中取
.在⑶中取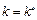 ,推得
,推得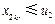 ,于是
,于是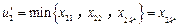 .下证对任意的
.下证对任意的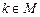 ,存在某个
,存在某个 ,2,3使得
,2,3使得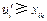 .假若不然,则
.假若不然,则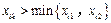 ,
, ,3且
,3且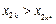 .这与
.这与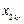 的最大性矛盾.因此,数表
的最大性矛盾.因此,数表 满足性质
满足性质 .
.下证唯一性.设有
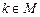 使得数表
使得数表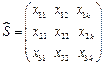
具有性质
 ,不失一般性,我们假定
,不失一般性,我们假定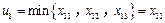
⑷
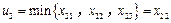
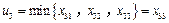
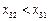 .
.由于
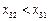 ,
,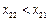 及(ⅰ),有
及(ⅰ),有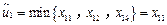 .又由(ⅰ)知:或者
.又由(ⅰ)知:或者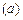
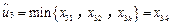 ,或者
,或者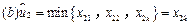 .
.如果
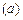 成立,由数表
成立,由数表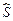 具有性质
具有性质 ,则
,则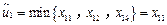 ,
,⑸
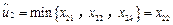 ,
,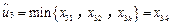 .
.由数表
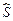 满足性质
满足性质 ,则对于
,则对于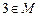 至少存在一个
至少存在一个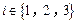 使得
使得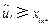 .由
.由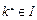 及⑷和⑹式知,
及⑷和⑹式知,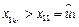 ,
,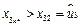 .于是只能有
.于是只能有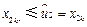 .类似地,由
.类似地,由 满足性质
满足性质 及
及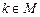 可推得
可推得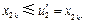 .从而
.从而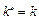 .
.
练习册系列答案
相关题目
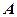 =
=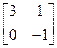 ,求
,求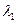 ,
,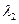 及对应的特征向量
及对应的特征向量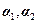 .
.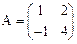 的特征值和对应的特征向量。
的特征值和对应的特征向量。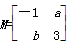 所对应的变换把直线l:2x-y=3变换为自身,
所对应的变换把直线l:2x-y=3变换为自身,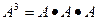 ,若矩阵
,若矩阵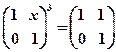 ,则
,则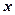 的值是_____________.
的值是_____________.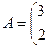
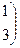 的逆矩阵
的逆矩阵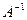 = 。
= 。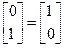 ,M
,M =,求M
=,求M