��Ŀ����
11��Ϊ���о�ij��ϸ����ʱ��x�仯����ֳ�ĸ������ռ��������£�| ����x/�� | 1 | 2 | 3 | 4 | 5 | 6 |
| ��ֳ����y/�� | 6 | 12 | 25 | 49 | 95 | 190 |
| $\overline x$ | $\overline y$ | $\overline z$ | $\sum_{i=1}^6{��{x_i}-\overline x}{��^2}$ | $\sum_{i=1}^6{��{x_i}-\overline x}����{y_i}-\overline y��$ | $\sum_{i=1}^6{��{x_i}-\overline x}����{z_i}-\overline z��$ |
| 3.5 | 6283 | 3.53 | 17.5 | 596.505 | 12.04 |
��2�����ݣ�1�����ж���ѽ�������е����ݣ�����y����x �Ļع鷽�̣�
�ο���ʽ��$b=\frac{{\sum_{i=1}^n{��{x_i}-\overline x����{y_i}-\overline y��}}}{{\sum_{i=1}^n{{{��{x_i}-\overline x��}^2}}}}$$a=\overline y-b\overline x$��
���� ��1�������ռ����ݣ��ɵ����ݵ�ɢ��ͼ��
��2����ɢ��ͼ����������ֲ���һ��ָ��������y=cebx��c��0������Χ����lny=bx+lnc���任���������ֲ���һ��ֱ�߸�������˿��������Իع鷽������ϣ��������y��x�Ļع鷽�̣�
��� �⣺��1������ɢ��ͼ��ͼ1��ʾ��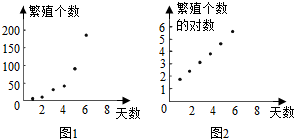
��ɢ��ͼ����������ֲ���һ��ָ������y=${C_1}{e^{{C_2}x}}$����Χ������ѡ��y=${C_1}{e^{{C_2}x}}$
��2����Z=lny����$\hat Z=bX+a$
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| Z | 1.79 | 2.48 | 3.22 | 3.89 | 4.55 | 5.25 |
��ͼ2���Կ������任���������ֲ���һ��ֱ�߸�������˿��������Իع鷽������ϣ�
��$b=\frac{{\sum_{i=1}^6{��{x_i}-\overline x����{z_i}-\overline z��}}}{{\sum_{i=1}^6{{{��{x_i}-\overline x��}^2}}}}$=$\frac{12.04}{17.5}=0.688$��$a=\overline z-b\overline x$=1.122
��$\hat Z=0.688X+1.122$�� ����$\hat y={e^{0.688x+1.122}}$
���� ���⿼�����Իع鷽�̣�����ɢ��ͼ������ѧ�������������������������е��⣮

��ϰ��ϵ�д�
�����Ŀ
1���ڡ�ABC�У�a=4��b=7��sinB=$\frac{1}{4}$����sinA=��������
| A�� | $\frac{1}{7}$ | B�� | $\frac{7}{16}$ | C�� | $\frac{7}{8}$ | D�� | $\frac{4}{7}$ |
19���Ծ���������ع�ϵ�ı���x��y��һ��۲����ݣ�xi��yi����i=1��2����8������ع�ֱ�߷�����$\hat y=\frac{1}{3}$x+a����x1+x2+x3+��+x8=2��y1+y2+y3+��+y8��=6����ʵ��a��ֵ�ǣ�������
| A�� | $\frac{1}{16}$ | B�� | $\frac{1}{8}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{1}{2}$ |
