题目内容
【题目】已知椭圆![]() :
: ![]() 的左右焦点分别是
的左右焦点分别是![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,当
,当![]() 时,
时, ![]() 恰为椭圆
恰为椭圆![]() 的上顶点,此时
的上顶点,此时![]() 的面积为6.
的面积为6.

(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左顶点为
的左顶点为![]() ,直线
,直线![]() 与直线
与直线![]() 分别相交于点
分别相交于点![]() ,问当
,问当![]() 变化时,以线段
变化时,以线段![]() 为直径的圆被
为直径的圆被![]() 轴截得的弦长是否为定值?若是,求出这个定值,若不是,说明理由.
轴截得的弦长是否为定值?若是,求出这个定值,若不是,说明理由.
【答案】(1)![]() ;(2)弦长为定值6.
;(2)弦长为定值6.
【解析】试题分析:(1)根据![]() 时,直线的倾斜角为
时,直线的倾斜角为![]() ,又
,又![]() 的周长为6,即可求得椭圆方程;(2)利用特殊位置猜想结论:当
的周长为6,即可求得椭圆方程;(2)利用特殊位置猜想结论:当![]() 时,直线
时,直线![]() 的方程为:
的方程为: ![]() ,求得以
,求得以![]() 为直径的圆过右焦点,被
为直径的圆过右焦点,被![]() 轴截得的弦长为6 ,猜测当
轴截得的弦长为6 ,猜测当![]() 变化时,以
变化时,以![]() 为直径的圆恒过焦点
为直径的圆恒过焦点![]() ,被
,被![]() 轴截得的弦长为定值6,再进行证明即可.
轴截得的弦长为定值6,再进行证明即可.
试题解析:(1)当![]() 时,直线的倾斜角为
时,直线的倾斜角为![]() ,所以:
,所以: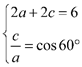
解得: ![]() ,所以椭圆方程是:
,所以椭圆方程是:![]() ;
;
(2)当![]() 时,直线
时,直线![]() :
: ![]() ,此时,
,此时,![]() ,
,![]() ,又
,又![]() 点坐标是
点坐标是![]() ,据此
,据此
可得![]() ,
,![]() ,故以
,故以![]() 为直径的圆过右焦点,被
为直径的圆过右焦点,被![]() 轴截得的弦长为6.由此猜测当
轴截得的弦长为6.由此猜测当![]() 变化时,以
变化时,以![]() 为直径的圆恒过焦点
为直径的圆恒过焦点![]() ,被
,被![]() 轴截得的弦长为定值6.
轴截得的弦长为定值6.
证明如下:设点![]() 点的坐标分别是
点的坐标分别是![]() ,则直线
,则直线![]() 的方程是:
的方程是:
![]() ,所以点
,所以点![]() 的坐标是
的坐标是![]() ,同理,点
,同理,点![]() 的坐标是
的坐标是![]() ,
,
由方程组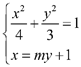 得到:
得到:![]() ,
,
所以:![]() , 从而:
, 从而:
![]()
![]() =0,
=0,
所以:以![]() 为直径的圆一定过右焦点
为直径的圆一定过右焦点![]() ,被
,被![]() 轴截得的弦长为定值6.
轴截得的弦长为定值6.

【题目】2014年7月16日,中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》,报告显示:我国网络购物用户已达![]() 亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为
亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为![]() .
.

(Ⅰ)确定![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)为进一步了解网购金额的多少是否与网龄有关,对这100名网购者调查显示:购物金额在2000元以上的网购者中网龄3年以上的有35人,购物金额在2000元以下(含2000元)的网购者中网龄不足3年的有20人.
①请将列联表补充完整;
网龄3年以上 | 网龄不足3年 | 合计 | |
购物金额在2000元以上 | 35 | ||
购物金额在2000元以下 | 20 | ||
合计 | 100 |
②并据此列联表判断,是否有![]() %的把握认为网购金额超过2000元与网龄在三年以上有关?
%的把握认为网购金额超过2000元与网龄在三年以上有关?
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式:  ,其中
,其中![]() )
)
【题目】某品牌汽车4s店对最近100位采用分期付款的购车者进行统计,统计结果如表所示:
付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
频数 | 40 | 20 | a | 10 | b |
已知分3期付款的频率为0.2,4s店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元,分2期或3期付款其利润为1.5万元,分4期或5期付款,其利润为2万元,用Y表示经销一辆汽车的利润.
(1)求上表中a,b的值.
(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有一位采用3期付款”的概率P(A)
(3)求Y的分布列及数学期望EY.