题目内容
如图,在四面体ABOC中,OC⊥OA。OC⊥OB,∠AOB=120°,且OA=OB=OC=1
(Ⅰ)设P为AC的中点,Q在AB上且AB=3AQ,证明:PQ⊥OA;
(Ⅱ)求二面角O-AC-B的平面角的余弦值。

(Ⅰ)设P为AC的中点,Q在AB上且AB=3AQ,证明:PQ⊥OA;
(Ⅱ)求二面角O-AC-B的平面角的余弦值。


(Ⅰ)在平面OAB内作ON OA交AB于N,连接CN,在△AOB中,
OA交AB于N,连接CN,在△AOB中,
 且OA=OB,
且OA=OB, 。在Rt△AON中,
。在Rt△AON中,
 ,
, 。
。


在△ONB中,
 .
. 。又AB=3AQ,
。又AB=3AQ, Q为AN的中点。在△CAN中,
Q为AN的中点。在△CAN中, 分别为AC,AN的中点,
分别为AC,AN的中点, .由OA
.由OA OC,OA
OC,OA ON知:OA
ON知:OA 平面CON。又NC
平面CON。又NC 平面CON,
平面CON, OA
OA CN.由PQ//CN,知OA
CN.由PQ//CN,知OA PQ.
PQ. 
(Ⅱ)连结PN,PO.
由OC OA,OC
OA,OC OB知:OC
OB知:OC 平面OAB。
平面OAB。
又ON 平面OAB,
平面OAB, OC
OC ON.又由ON
ON.又由ON OA知:ON
OA知:ON 平面AOC.
平面AOC.  OP是NP在平面AOC内的射影。
OP是NP在平面AOC内的射影。
在等腰Rt△COA中,P为AC的中点, AC
AC OP。
OP。
根据三垂线定理,知:AC NP.
NP.

 为二面角O-AC-B的平面角。
为二面角O-AC-B的平面角。
在等腰Rt△COA中,OC="OA=1," OP=
OP= 。
。
在Rt△AON中,ON=OA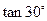 =
= ,
,
 在Rt△PON中,PN=
在Rt△PON中,PN=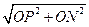 =
= ,
,
 cos
cos 。
。
解法二:
(Ⅰ)取O为坐标原点,以OA,OC所在的直线为x轴,z轴,建立空间直角坐标系O-xyz(如图所示)。
则A(1,0,0),C(0,0,1),B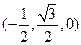 。
。
 。
。 。
。
又由已知,可得
又 .
. .
.
 .故
.故 。
。
(Ⅱ)记平面ABC的法向量 ,则由n
,则由n
 ,n
,n ,且
,且 =(1,0,-1)。
=(1,0,-1)。
得 故可取
故可取 。
。
又平面OAC的法向量为e=(0,1,0)。

二面角O-AC-B的平面角是锐角,记为 ,则
,则 。
。
 OA交AB于N,连接CN,在△AOB中,
OA交AB于N,连接CN,在△AOB中,
 且OA=OB,
且OA=OB, 。在Rt△AON中,
。在Rt△AON中,
 ,
, 。
。

在△ONB中,

 .
. 。又AB=3AQ,
。又AB=3AQ, Q为AN的中点。在△CAN中,
Q为AN的中点。在△CAN中, 分别为AC,AN的中点,
分别为AC,AN的中点, .由OA
.由OA OC,OA
OC,OA ON知:OA
ON知:OA 平面CON。又NC
平面CON。又NC 平面CON,
平面CON, OA
OA CN.由PQ//CN,知OA
CN.由PQ//CN,知OA PQ.
PQ. 
(Ⅱ)连结PN,PO.
由OC
 OA,OC
OA,OC OB知:OC
OB知:OC 平面OAB。
平面OAB。又ON
 平面OAB,
平面OAB, OC
OC ON.又由ON
ON.又由ON OA知:ON
OA知:ON 平面AOC.
平面AOC.  OP是NP在平面AOC内的射影。
OP是NP在平面AOC内的射影。在等腰Rt△COA中,P为AC的中点,
 AC
AC OP。
OP。根据三垂线定理,知:AC
 NP.
NP.
 为二面角O-AC-B的平面角。
为二面角O-AC-B的平面角。在等腰Rt△COA中,OC="OA=1,"
 OP=
OP= 。
。在Rt△AON中,ON=OA
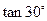 =
= ,
, 在Rt△PON中,PN=
在Rt△PON中,PN=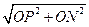 =
= ,
, cos
cos 。
。解法二:
(Ⅰ)取O为坐标原点,以OA,OC所在的直线为x轴,z轴,建立空间直角坐标系O-xyz(如图所示)。
则A(1,0,0),C(0,0,1),B
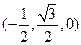 。
。
 。
。 。
。又由已知,可得

又
 .
. .
. .故
.故 。
。(Ⅱ)记平面ABC的法向量
 ,则由n
,则由n
 ,n
,n ,且
,且 =(1,0,-1)。
=(1,0,-1)。得
 故可取
故可取 。
。又平面OAC的法向量为e=(0,1,0)。

二面角O-AC-B的平面角是锐角,记为
 ,则
,则 。
。
练习册系列答案
相关题目
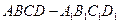 中,
中,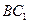 与对角面
与对角面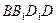 所成角的大小是________.
所成角的大小是________.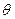 ,已知
,已知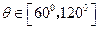 ,则AC、BD之间的距离的最大值和最小值 .
,则AC、BD之间的距离的最大值和最小值 . 中,二面角
中,二面角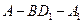 的度数是 .
的度数是 .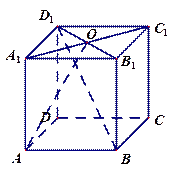
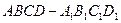 中,
中,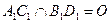 .
. 与
与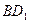 所成角的余弦值;
所成角的余弦值;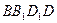 所成角的余弦值.
所成角的余弦值. ,则sin
,则sin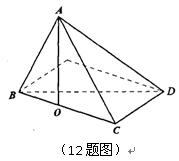

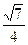
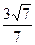


 的底面是边长为1的正方形,且侧棱垂直于底面,若
的底面是边长为1的正方形,且侧棱垂直于底面,若 与底面
与底面 成60°角,则二面角
成60°角,则二面角 的平面角的正切值为
的平面角的正切值为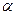 外一点
外一点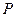 的斜线段是过这点垂线段的
的斜线段是过这点垂线段的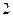 倍,则此斜线与平面
倍,则此斜线与平面


