题目内容
【题目】平面图形ABB1A1C1C如图4所示,其中BB1C1C是矩形,BC=2,BB1=4,AB=AC= ![]() ,A1B1=A1C1=
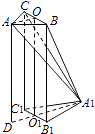
,A1B1=A1C1= ![]() .现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.
.现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.
(Ⅰ)证明:AA1⊥BC;
(Ⅱ)求AA1的长;
(Ⅲ)求二面角A﹣BC﹣A1的余弦值.
【答案】证明:(Ⅰ)取BC,B1C1的中点为点O,O1 , 连接AO,OO1 , A1O,A1O1 ,
∵AB=AC,∴AO⊥BC
∵平面ABC⊥平面BB1C1C,平面ABC∩平面BB1C1C=BC
∴AO⊥平面BB1C1C
同理A1O1⊥平面BB1C1C,∴AO∥A1O1 , ∴A、O、A1、O1共面
∵OO1⊥BC,AO⊥BC,OO1∩AO=O,∴BC⊥平面OO1A1A
∵AA1平面OO1A1A,∴AA1⊥BC;
(Ⅱ)解:延长A1O1到D,使O1D=OA,则∵O1D∥OA,∴AD∥OO1 , AD=OO1 ,
∵OO1⊥BC,平面A1B1C1⊥平面BB1C1C,平面A1B1C1∩平面BB1C1C=B1C1 ,
∴OO1⊥面A1B1C1 ,
∵AD∥OO1 ,
∴AD⊥面A1B1C1 ,
∵AD=BB1=4,A1D=A1O1+O1D=2+1=3
∴AA1= ![]() =5;
=5;
(Ⅲ)解:∵AO⊥BC,A1O⊥BC,∴∠AOA1是二面角A﹣BC﹣A1的平面角
在直角△OO1A1中,A1O= ![]()
在△OAA1中,cos∠AOA1=﹣ ![]()
∴二面角A﹣BC﹣A1的余弦值为﹣ ![]() .
.
【解析】(Ⅰ)证明AA1⊥BC,只需证明BC⊥平面OO1A1A,取BC,B1C1的中点为点O,O1 , 连接AO,OO1 , A1O,A1O1 , 即可证得;(Ⅱ)延长A1O1到D,使O1D=OA,则可得AD∥OO1 , AD=OO1 , 可证OO1⊥面A1B1C1 , 从而AD⊥面A1B1C1 , 即可求AA1的长;(Ⅲ)证明∠AOA1是二面角A﹣BC﹣A1的平面角,在△OAA1中,利用余弦定理,可求二面角A﹣BC﹣A1的余弦值.
【考点精析】本题主要考查了直线与平面垂直的性质和平面与平面垂直的性质的相关知识点,需要掌握垂直于同一个平面的两条直线平行;两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直才能正确解答此题.

【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到数据如表所示(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | 8 | |
不肥胖 | 18 | ||
合计 | 30 |
(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有99%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
| 0.050 0.010 |
| 3.841 6.635 |
参考数据:
附:![]()