题目内容
已知函数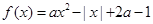 (
(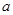 为实常数).
为实常数).
(1)若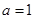 ,求
,求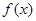 的单调区间;
的单调区间;
(2)若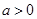 ,设
,设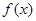 在区间
在区间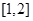 的最小值为
的最小值为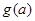 ,求
,求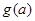 的表达式;
的表达式;
(3)设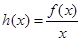 ,若函数
,若函数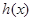 在区间
在区间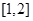 上是增函数,求实数
上是增函数,求实数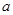 的取值范围.
的取值范围.
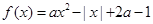 (
(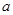 为实常数).
为实常数). (1)若
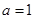 ,求
,求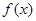 的单调区间;
的单调区间; (2)若
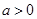 ,设
,设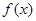 在区间
在区间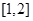 的最小值为
的最小值为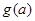 ,求
,求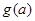 的表达式;
的表达式;(3)设
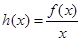 ,若函数
,若函数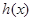 在区间
在区间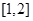 上是增函数,求实数
上是增函数,求实数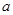 的取值范围.
的取值范围.(1)
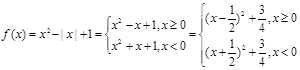 2分
2分
∴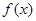 的单调增区间为(
的单调增区间为(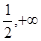 ),(-
),(-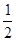 ,0)
,0) 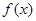 的单调减区间为(-
的单调减区间为(-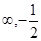 ),(
),(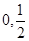 )
)
(2)由于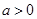 ,当
,当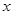 ∈[1,2]时,
∈[1,2]时,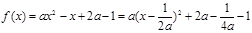 (1分)
(1分)
10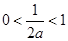 即
即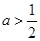
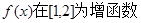
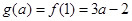 (1分)
(1分)
20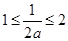 即
即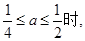
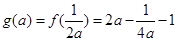 (1分)
(1分)
30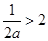 即
即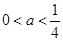 时
时 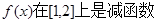
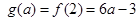 (1分)
(1分)
综上可得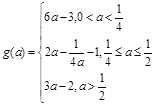 (1分)
(1分)
(3)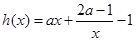 在区间[1,2]上任取
在区间[1,2]上任取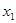 、
、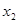 ,且
,且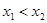
则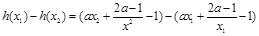
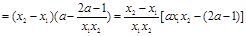 (*) ∵
(*) ∵
∴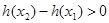 (2分)
(2分)
∴(*)可转化为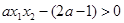 对任意
对任意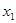 、
、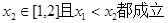
即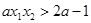 10 当
10 当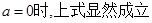
20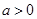
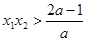 由
由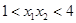 得
得 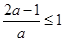 解得
解得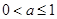
30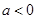
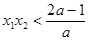
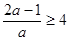 得
得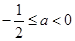
所以实数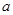 的取值范围是
的取值范围是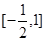

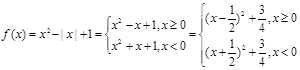 2分
2分∴
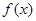 的单调增区间为(
的单调增区间为(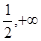 ),(-
),(-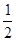 ,0)
,0) 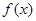 的单调减区间为(-
的单调减区间为(-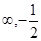 ),(
),(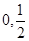 )
) (2)由于
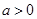 ,当
,当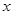 ∈[1,2]时,
∈[1,2]时,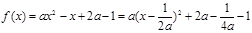 (1分)
(1分)10
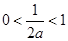 即
即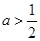
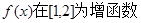
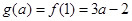 (1分)
(1分)20
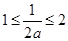 即
即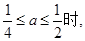
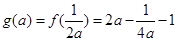 (1分)
(1分)30
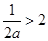 即
即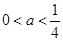 时
时 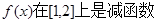
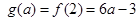 (1分)
(1分)综上可得
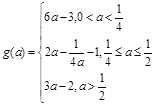 (1分)
(1分)(3)
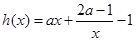 在区间[1,2]上任取
在区间[1,2]上任取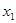 、
、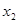 ,且
,且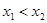
则
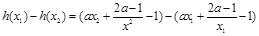
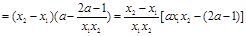 (*) ∵
(*) ∵
∴
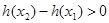 (2分)
(2分)∴(*)可转化为
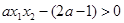 对任意
对任意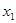 、
、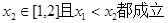
即
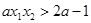 10 当
10 当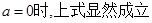
20
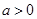
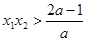 由
由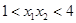 得
得 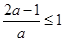 解得
解得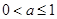
30
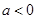
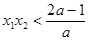
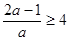 得
得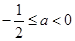
所以实数
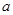 的取值范围是
的取值范围是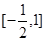
略

练习册系列答案
相关题目
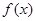 是R上的单调函数,且"x∈R,
是R上的单调函数,且"x∈R,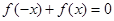 ,若
,若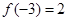
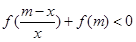 ,其中m∈R且m > 0
,其中m∈R且m > 0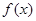 在
在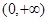 上是减函数,则下列关系式中成立的是( )
上是减函数,则下列关系式中成立的是( )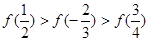
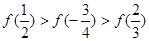
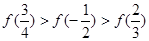
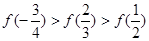
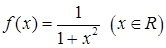 的值域是( )
的值域是( )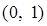
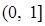
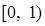
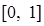
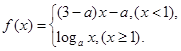 是
是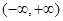 上的增函数,那么实数a的取值范围是( )
上的增函数,那么实数a的取值范围是( )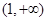
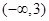
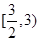
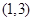
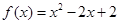 (
(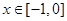 )的最小值是 ( )
)的最小值是 ( )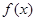 是定义在
是定义在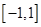 上的增函数,且
上的增函数,且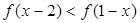 ,则
,则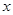 的取值范围为
的取值范围为