题目内容
【题目】已知圆
，直线过点
，且
，线段
交圆
的交点为点
，
是关于轴的对称点.
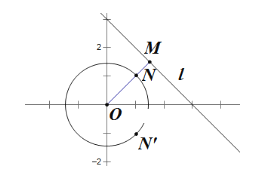
（1）求直线
的方程；
（2）已知
是圆上不同的两点，且
，试证明直线
的斜率为定值，并求出该定值.
【答案】（1）
；（2）证明见解析. 定值1.
【解析】
（1）由OM⊥l，得直线l的斜率为﹣1，由此求出直线l的方程，从而能求出结果．（2）已知A，B是圆O上不同的两点，且∠ANN'＝∠BNN'，设直线
的方程为：
，直线
的方程为：
，与圆联立求出A，B的坐标，即可证明直线AB的斜率为定值．
（1）由题
∵
，∴直线l的斜率为-1，
∴直线的方程为：
，即
.
（2）据题意直线OM:y=x,与圆联立可得
，
∵
是
关于轴的对称点，
，∴
，设
，则
，
则直线的方程为：，直线的方程为：，
联立
，消去
得：
，
∵
，∴
，同理可求
，
，
故直线
的斜率为定值1.
练习册系列答案
相关题目
【题目】柴静《穹顶之下》的播出，让大家对雾霾天气的危害有了更进一步的认识，对于雾霾天气的研究也渐渐活跃起来，某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析，得出下表数据：
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)请画出上表数据的散点图；
(2)请根据上表提供的数据，用最小二乘法求出
关于
的线性回归方程
；
(3)试根据(2)求出的线性回归方程，预测燃放烟花爆竹的天数为
的雾霾天数．
