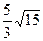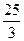题目内容
(本小题满分14分)在直角坐标系xoy中,已知三点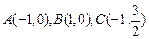
以A、B为焦点的椭圆经过C点,
(1) 求椭圆方程;
(2) 设点D(0,1),是否存在不平行于x轴的直线l,与椭圆交于不同的两点M、N,使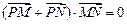 ?
?
若存在。求出直线l斜率的取值范围;
⑶对于y轴上的点P(0,n)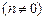 ,存在不平行于x轴的直线l与椭圆交于不同两点M、N,使
,存在不平行于x轴的直线l与椭圆交于不同两点M、N,使
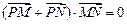 ,试求实数n的取值范围。
,试求实数n的取值范围。
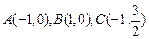
以A、B为焦点的椭圆经过C点,
(1) 求椭圆方程;
(2) 设点D(0,1),是否存在不平行于x轴的直线l,与椭圆交于不同的两点M、N,使
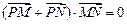 ?
?若存在。求出直线l斜率的取值范围;
⑶对于y轴上的点P(0,n)
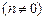 ,存在不平行于x轴的直线l与椭圆交于不同两点M、N,使
,存在不平行于x轴的直线l与椭圆交于不同两点M、N,使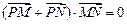 ,试求实数n的取值范围。
,试求实数n的取值范围。(1)
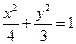
(2)符合条件的直线不存在
(3)
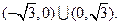
解:(1)设椭圆方程为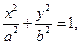 由焦点
由焦点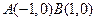 及椭圆过
及椭圆过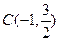 可得,
可得,
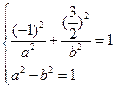 ,解得
,解得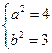 ,即椭圆方程是
,即椭圆方程是
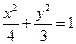 。 ……4分
。 ……4分
(2)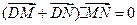 可知
可知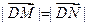 ,由题知直线的斜率存在。可设直线方程为
,由题知直线的斜率存在。可设直线方程为
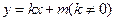 ,设
,设 的
的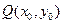 .
.
由题知 可得
可得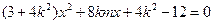 ,
,
可得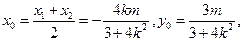 由
由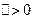 可得
可得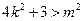 ,
,
由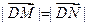 可得
可得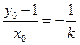 ,即
,即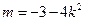 ,又由
,又由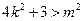 可得
可得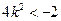 矛盾。所以符合条件的直线不存在。 ……10分
矛盾。所以符合条件的直线不存在。 ……10分
(3)由(2)知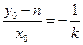 可推出
可推出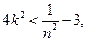 要使k存在只需
要使k存在只需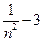
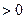 ,
,
解得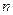 的取值范围是
的取值范围是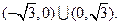
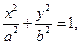 由焦点
由焦点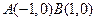 及椭圆过
及椭圆过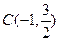 可得,
可得,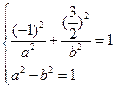 ,解得
,解得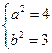 ,即椭圆方程是
,即椭圆方程是
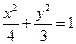 。 ……4分
。 ……4分(2)
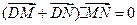 可知
可知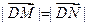 ,由题知直线的斜率存在。可设直线方程为
,由题知直线的斜率存在。可设直线方程为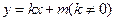 ,设
,设 的
的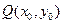 .
.由题知
 可得
可得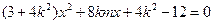 ,
,可得
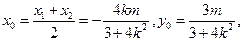 由
由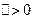 可得
可得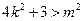 ,
,由
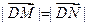 可得
可得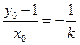 ,即
,即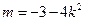 ,又由
,又由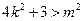 可得
可得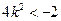 矛盾。所以符合条件的直线不存在。 ……10分
矛盾。所以符合条件的直线不存在。 ……10分(3)由(2)知
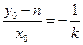 可推出
可推出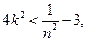 要使k存在只需
要使k存在只需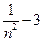
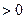 ,
,解得
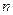 的取值范围是
的取值范围是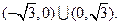

练习册系列答案
相关题目
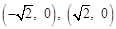 ,则
,则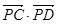 的最大值为 .
的最大值为 .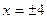 ,离心率等于
,离心率等于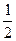 的椭圆方程是 .
的椭圆方程是 .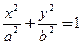 (
(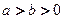 )的长轴,若把AB给100等分,过每个分点作AB的垂线,交椭圆的上半部分于P1、P2、… 、P99 ,F1为椭圆的左焦点,则
)的长轴,若把AB给100等分,过每个分点作AB的垂线,交椭圆的上半部分于P1、P2、… 、P99 ,F1为椭圆的左焦点,则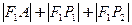 +…
+…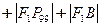 的值是__________.
的值是__________.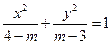 表示焦点在
表示焦点在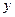 轴上的椭圆,则
轴上的椭圆,则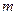 的取值范围是 .
的取值范围是 . 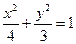 的左、右焦点分别为F1、F2, P为椭圆上一点, 且∠F1PF2=60°,
的左、右焦点分别为F1、F2, P为椭圆上一点, 且∠F1PF2=60°,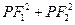 的值为 ▲
的值为 ▲ 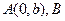 为椭圆
为椭圆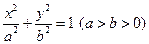 的左准线与
的左准线与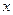 轴的交点.若线段
轴的交点.若线段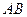 的中点
的中点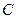 在椭圆上,则该椭圆的离心率为
在椭圆上,则该椭圆的离心率为 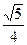

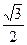
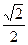
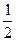
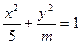 的离心率
的离心率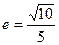 ,则
,则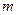 的值为 ( )
的值为 ( )
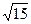 或
或