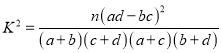题目内容
【题目】将2张边长均为1分米的正方形纸片分别按甲、乙两种方式剪裁并废弃阴影部分.
(1)在图甲的方式下,剩余部分恰能完全覆盖某圆锥的表面,求该圆锥的母线长及底面
半径;
(2)在图乙的方式下,剩余部分能完全覆盖一个长方体的表面,求长方体体积的最大值.

【答案】(1)![]() 分米,
分米, ![]() 分米.(2)
分米.(2)![]() 立方分米.
立方分米.
【解析】试题分析:(1)设圆锥母线为l,圆锥底面圆半径为r,则有![]() ,
, ![]() 可解得l.r.
可解得l.r.
(2)设长方体的棱长为x,y,z,则![]() 可得
可得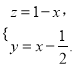 所以长方体的体积
所以长方体的体积![]() ,
, ![]() 利用导数可求得其最大值.
利用导数可求得其最大值.
试题解析:(1)设圆锥的母线长及底面半径分别为![]() ,
,
则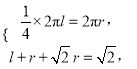
解得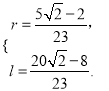

(2)设被完全覆盖的长方体底面边长为![]() ,宽为
,宽为![]() ,高为
,高为![]() ,
,
则![]()
解得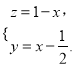
则长方体的体积:
![]() ,
, ![]()
所以![]() .令
.令![]() 得,
得, ![]() 或
或![]() (舍去).
(舍去).
列表:

所以,当![]() 时,
时, ![]() .
.

【题目】设函数![]() .
.
(1)若函数![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(2)设函数![]() ,若对任意的
,若对任意的![]() ,都有
,都有![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)设![]() ,点
,点![]() 是函数
是函数![]() 与
与![]() 的一个交点,且函数
的一个交点,且函数![]() 与
与![]() 在点
在点![]() 处的切线互相垂直,求证:存在唯一的
处的切线互相垂直,求证:存在唯一的![]() 满足题意,且
满足题意,且![]() .
.
【题目】“微信运动”已成为当下热门的运动方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
步数 性别 | 0-2000 | 2001-5000 | 5001-8000 | 8001-10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
附: 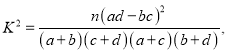
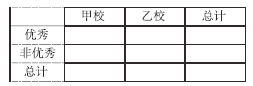
(1)已知某人一天的走路步数超过8000步被系统评定为“积极型”,否则为“懈怠型”,根据题意完成下面的 积极型 懈怠型 总计 男 女 总计 (2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.