题目内容
【题目】如图,ABCD与ADEF为平行四边形,M,N,G分别是AB,AD,EF的中点.求证: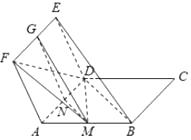
(1)BE∥平面DMF;
(2)平面BDE∥平面MNG.
【答案】
(1)证明:如图,
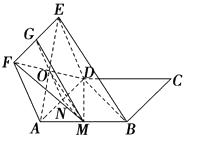
连接AE,则AE必过DF与GN的交点O,连接MO,
则MO为△ABE的中位线,所以BE∥MO,
又BE平面DMF,MO平面DMF,所以BE∥平面DMF
(2)证明:因为N,G分别为平行四边形ADEF的边AD,EF的中点,所以DE∥GN,
又DE平面MNG,GN平面MNG,所以DE∥平面MNG.
又M为AB中点,所以MN为△ABD的中位线,所以BD∥MN,
又BD平面MNG,MN平面MNG,所以BD∥平面MNG,又DE与BD为平面BDE 内的两条相交直线, 所以平面BDE∥平面MNG
【解析】本题抓住几个关键词解题:1.“ABCD与ADEF为平行四边形”得到相关平行直线;2.“,M,N,G分别是AB,AD,EF的中点”想到三角形中位线或者构造平行四边形。3.找关键做辅助线。4.做题思路:由线线平行![]() 线面平行
线面平行![]() 面面平行。
面面平行。
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和直线与平面平行的性质的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;简记为:线面平行则线线平行.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目