题目内容
设各项为正的数列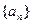 ,其前
,其前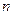 项和为
项和为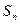 ,并且对所有正整数
,并且对所有正整数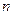 ,
,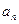 与2的等差中项等于
与2的等差中项等于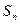 与2的等比中项.
与2的等比中项.
(1)写出数列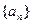 的前二项;
的前二项;
(2)求数列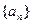 的通项公式(写出推证过程);
的通项公式(写出推证过程);
(3)令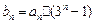 ,求
,求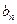 的前
的前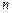 项和
项和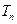 .
.
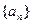 ,其前
,其前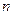 项和为
项和为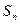 ,并且对所有正整数
,并且对所有正整数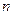 ,
,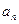 与2的等差中项等于
与2的等差中项等于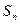 与2的等比中项.
与2的等比中项.(1)写出数列
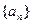 的前二项;
的前二项; (2)求数列
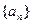 的通项公式(写出推证过程);
的通项公式(写出推证过程);(3)令
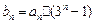 ,求
,求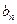 的前
的前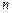 项和
项和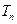 .
.解:(1)由题意可
 得
得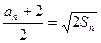 ,∴
,∴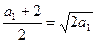 ,解得:
,解得: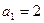 ; (2分)
; (2分)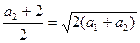 ,解得:
,解得: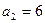 ; (4分)
; (4分)(2)由
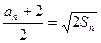 得
得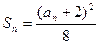 ,当
,当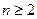 时,
时,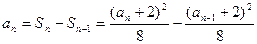 ,化简得:
,化简得: 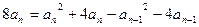
即
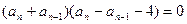 又
又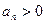 ∴
∴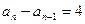 , (7分)
, (7分)因此数列
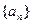 是以2为首项,4为公差的等差数列,故
是以2为首项,4为公差的等差数列,故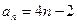 (8分)
(8分)(3)由
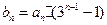 ,得
,得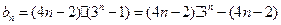
记
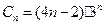 ,其
,其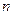 项和记为
项和记为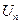 ,则
,则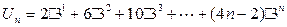 , ……①
, ……① 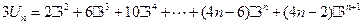 ,……②
,……② ①-② 得
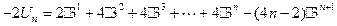
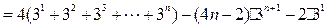
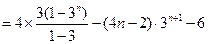
∴
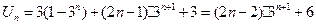 (11分)
(11分)∴
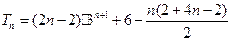
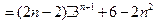 (12分)
(12分)略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
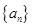 中,
中,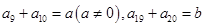 ,则
,则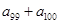 等于
等于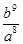 B.
B. 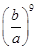 C.
C. 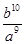 D
D 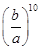
 ,
, ,
, ,则
,则



 中,
中, =0,且对任意k
=0,且对任意k ,
, 成等差数列,
成等差数列, 成等比数列;
成等比数列; 的通项公式;
的通项公式;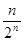 ,则前n项和为 ( )
,则前n项和为 ( )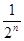
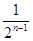 -
- 若
若 的最小值为( )
的最小值为( )
 的前
的前 项和为
项和为 ,且
,且
 ,
, 及
及 ;(2)证明:数列
;(2)证明:数列 .
. 是等比数列,
是等比数列, ,则
,则 =__________.
=__________.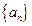 满足
满足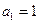 ,
,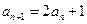 ,若数列
,若数列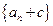 恰为等比数列,则
恰为等比数列,则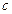 的值为 .
的值为 .