题目内容
在平面直角坐标系xOy中,设点P(x1,y1)、Q(x2,y2),定义:d(P,Q)=|x1-x2|+|y1-y2|.已知点B(1,0),点M为直线x-2y+2=0上的动点,则使d(B,M)取最小值时点M的坐标是______.
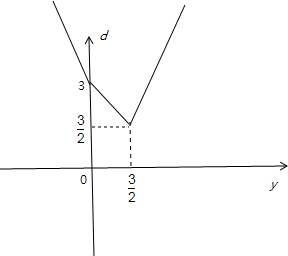
设M(2y-2,y),由题意d(B,M)=|2y-2-1|+|y-0|=|2y-3|+|y|=
,
显然y=
时d(B,M)取最小值,此时M(1,
)
故答案为:(1,
)
|
显然y=
| 3 |
| 2 |
| 3 |
| 2 |
故答案为:(1,
| 3 |
| 2 |


练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
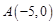 ,
,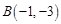 ,若圆
,若圆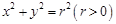 上恰有两点
上恰有两点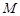 ,
,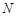 ,使得
,使得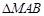 和
和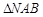 的面积均为
的面积均为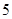 ,则
,则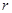 的取值范围是 .
的取值范围是 .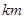 的圆形村落,A、B两人同时从村落中心出发,B向北直行,A先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B相遇.设A、B两人速度一定,其速度比为3:1,问两人在何处相遇?
的圆形村落,A、B两人同时从村落中心出发,B向北直行,A先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B相遇.设A、B两人速度一定,其速度比为3:1,问两人在何处相遇?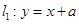 和
和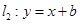 将单位圆
将单位圆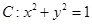 分成长度相等的四段弧,则
分成长度相等的四段弧,则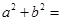 .
.