题目内容
直线y=x+b与抛物线x2=2y交于A、B两点,O为坐标原点,且OA⊥OB,则b的值是( )
A.2 B.-2
C.1 D.-1
A.2 B.-2
C.1 D.-1
A
设A(x1,y1)、B(x2,y2),将y=x+b代入x2=2y得x2-2x-2b=0.则x1x2=?-2b?,x1+x2=2.
∴y1y2=(x1+b)(x2+b)=x1x2+b(x1+x2)+b2=b2.
由OA⊥OB,得x1x2+y1y2=0,即-2b+b2=0.∴b=0(舍去)或2.
又Δ=22+8b>0,得b>-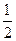 .∴b=2符合.
.∴b=2符合.
∴y1y2=(x1+b)(x2+b)=x1x2+b(x1+x2)+b2=b2.
由OA⊥OB,得x1x2+y1y2=0,即-2b+b2=0.∴b=0(舍去)或2.
又Δ=22+8b>0,得b>-
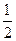 .∴b=2符合.
.∴b=2符合.
练习册系列答案
相关题目
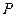 到点
到点 的距离比它到直线
的距离比它到直线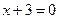 的距离小1,则点
的距离小1,则点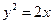



 )
) )
)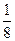
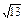 ,一直角边的方程是y=2x,求抛物线的方程.
,一直角边的方程是y=2x,求抛物线的方程.